Fast Synthesis of Dynamic Colour Textures

by Jiři Filip, Michal Haindl and Dmitry Chetverikov

The textural appearance of many real-world materials is not static, but changes over time. If such change is spatially and temporally homogeneous, these materials can be represented by means of dynamic textures (DT). DT modelling is a challenging problem that can improve the quality of computer graphics applications. As part of the MUSCLE Network of Excellence, collaboration between three ERCIM members - CRCIM-UTIA, SZTAKI and CWI - has developed a novel hybrid method for colour DT modelling.

Dynamic or temporal textures (DT) can be defined as spatially repetitive motion patterns exhibiting stationary temporal properties and having indeterminable spatial and temporal contents. The surface of water, fire and straw in the wind are typical DT examples. As a basic representation of DTs, a video sequence has finite duration. This limits the use of DTs in virtual reality systems of any kind, making temporally unconstrained modelling of DT a challenging problem for research areas such as computer vision, pattern recognition and computer graphics. Previous DT modelling approaches were based either on video editing techniques or time-consuming mathematical models, which were generally restricted to greyscale DT modelling.

The proposed method shows good performance for most of the tested DTs: this depends mainly on the properties of the original sequence. Moreover, this method significantly compresses the original data and enables high-speed synthesis of unlimited artificial sequences, which is easily performed by means of contemporary graphics hardware.

The method, illustrated in Figure 1, is based on a combination of input data dimensionality reduction using the eigen-analysis, and the subsequent modelling of resulting temporal coefficients by means of a causal simultaneous auto-regressive random field model (CAR). The model is learned from real measured DTs (typically 250-frame video sequences). Measured data often show spatial discontinuity between successive images in DT sequences of very fast processes. Furthermore, available sequences are usually too short for robust statistical estimation of model parameters. We therefore performed the interpolation of individual temporal coefficients by means of cubic splines. This pre-processing step generates additional frames between each pair of original frames and improves the learning quality of the un

derlying random field model. The major advantage of the CAR model is that it can be solved analytically under several additional and acceptable assumptions.

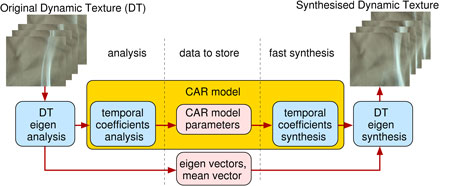Figure 1: Scheme of the proposed dynamic texture hybrid model.

The CAR model synthesis is very simple. New temporal mixing coefficients of individual eigen-images can be directly generated from the model equation using the estimated model parametric matrix and a multivariate Gaussian generator with estimated noise variance. Both the synthesis of new temporal coefficients and the following interpolation of eigen-images can be performed at even faster rates using contemporary graphics hardware programming. Moreover, this technique enables significant compression of the original DT data, typically at a ratio of between 1:5 and 1:10 depending on the length and the character of the DT sequence. The method was verified visually and by using two proposed statistical similarity measures on dynamic texture data sets. These include fire, boiling water, moving escalators, smoke, straw etc, and are taken from the DynTex texture database maintained by our partners at CWI. The comparison of original and synthesized DT frames of natural textures is shown in Figure 2. The corresponding results for the man-made textures are illustrated in Figure 3. The analysis time of the original DT was about three minutes. The synthesis of a new DT sequence is very fast (about 60 frames/s using non-optimized CPU software implementation on a PC with an Athlon 2GHz processor), and the generation time can be further improved using the programmable processing unit of a contemporary graphics card.

Figure 2: Examples of frames from original DT (odd rows) and the corresponding synthesised frames using the proposed model (even rows) for three natural DTs.	Figure 3: Examples of frames from original DT (odd rows) and the corresponding synthesised frames using the proposed model (even rows) for two man made DTs.

Links:
DTdemos: http://ro.utia.cz/demos/DTsynth.html
DynTex database: http://www.cwi.nl/projects/dyntex/
http://ieeexplore.ieee.org/Xplore/guesthome.jsp (see IEEE Digital Library for the article).

Please contact:
Jiří Filip, Institute of Information Theory and Automation, Academy of Sciences / CRCIM, Czech Republic
Dmitry Chetverikov, SZTAKI, Hungary
Tel: +420 266052365
E-mail: filipjutia.cas.cz