Reconstruction, Modelling and Motion Analysis of the Human Knee Based on Magnetic Resonance Images

by Gábor Renner and György Szántó

New computer methods and programs have been developed at SZTAKI in cooperation with the Orthopaedic Department of the Semmelweis University and the CT/MR Laboratory of the International Medical Center, Budapest. They support the three-dimensional visualization, reconstruction and modelling of the tissues and organs of the human body. These methods were used in examining the morphology and movement of the knee.

The knee joint is a very delicate and frequently damaged component of the human motion system. A wide range of imaging techniques (MR, CT) is available to clinical practitioners investigating the injured parts. These methods offer invaluable support to the orthopaedic surgeon by making visible both the state of the articular cartilage and certain joint diseases. The same tools can be applied to the analysis of kinematic behaviour as well as the morphology of the articular cartilage.

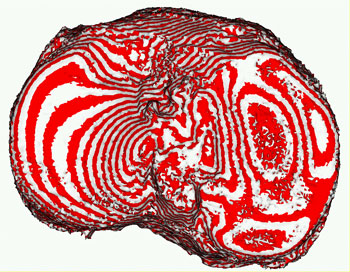
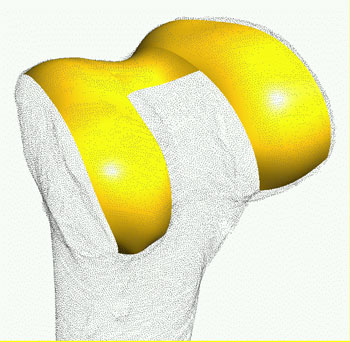
When analysing articular motion, the determination of the contact points (regions) of the cartilage surfaces in three-dimensional (3D) space is especially important. Delineation of the contacting surfaces is extremely difficult due firstly to the similar grey-scale representation of the synovial fluid between the opposite surfaces and the hyalin, and secondly to the fact that the two surfaces are partly covering each other. We have developed computer methods for the image analysis, the 3D reconstruction, and for building geometric models of the knee joint based on MR/CT images. An iso-surface ray-tracing method with a Phong illumination model is used to create surfaces from volume grid models according to a predefined value of grey-scale threshold.

Surface points extracted from the iso-surface models represent only rough information on the shape. Accurate geometrical models are required for a detailed analysis of the shape and functionality of the knee structures, especially when studying the contact properties of proximal or touching cartilage surfaces.
Spatial geometrical models are created using a set of contours extracted from MR images. We have developed active contour and fast marching methods for the detection of tissue contours in the sequence of MR images relevant to the knee joint (bone, cartilage). Our algorithms and programs based on these two methods work fast and reliably for bone contours; however, they require several improvements for cartilage contours.

By using contours extracted from 2D images and suitable transformations, a digitized representation (point set) of functional surfaces of the knee joint can be constructed. We have developed several methods and programs, which allow us to visualize and evaluate the morphology of those surfaces (eg noise elimination, decimation and triangulation). Various geometrical properties (eg lines of intersection, curvature distributions and feature points) can be calculated, visualized and evaluated.

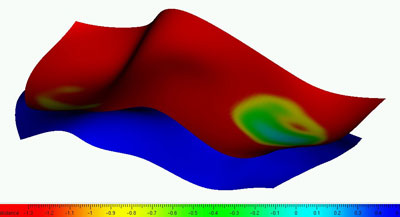
The study of the knee in motion is important both from anatomical and pathological points of view. This requires the alignment of images and spatial models corresponding to different flexions of the knee in a common coordinate system (registration). Different types of registration methods (such as iterative closest point methods and methods based on anatomical markers or feature points) have been developed for the accurate and fast registration of knee structures.

Our experiments show that continuous and smooth representations of the active surfaces are needed for detailed biological or medical investigations (especially for estimating the size and shape of the contacting regions of cartilages).

Continuous surface fit starts with the topological ordering of points, which is done by creating a triangulation over the surface points. A good triangulation must meet a number of requirements: it must be topologically correct, must eliminate outlier points, triangles must have comparable side lengths and angles, their size must reflect the curvatures of the surface, and so forth. Algorithms and computer programs have been developed for the automatic generation of triangular structures. The mathematical description of surfaces with a high degree of continuity is performed by parametric surfaces commonly used in computer graphics and CAD (eg Bézier, B-spline and NURBS surfaces). The mathematical representation of continuous surfaces is computed by minimizing a functional. This contains the squared distances of data points to the continuous surface, as well as geometrical quantities reflecting continuity and smoothness.

Contact properties of cartilage surfaces (their shape and extension) can be best evaluated by a distance function defined between the two surfaces. This is the length of the shortest path from a surface point to the other surface. We have developed a procedure to evaluate the distance function for the continuous surface models of the cartilage. Surfaces can be colour-coded according to the distance function, which provides an extremely efficient tool for evaluating the shape and size of the contact regions. Figure 3 shows the colour-coded distances for the two contacting cartilage surfaces (femur and tibia).

The above methods provide the basis for a prototype system to be used in the surgical treatment of orthopaedic patients. The complex nature of the problems in this area means that close cooperation is required within a multi-disciplinary team. The project, which has run from 2002-2005, has been greatly supported by the National Research and Development Programme of the Ministry of Education of Hungary.

Please contact:
Gábor Renner, SZTAKI, Hungary
Tel: +36 1 279 6152
E-mail: rennersztaki.hu

György Szántó , SZTAKI, Hungary
Tel: +36 1 279 6187
E-mail: szantosztaki.hu