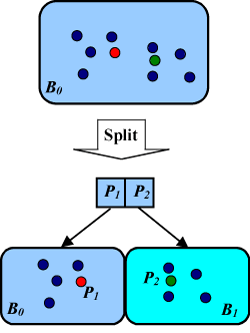
| |
GHT*: A Peer-to-Peer System for Metric Data
by Michal Batko, Claudio Gennaro and Pavel Zezula
GHT* is a scalable and distributed similarity search structure that has been specifically designed to support metric space objects. The structure is based on the Peer-to-Peer (P2P) communication paradigm. It is scalable, which means that the query execution achieves practically constant search time for similarity range queries in data-sets of arbitrary size. Updates are performed locally and node splitting does not require sending multiple messages to many peers.
P2P communication paradigms are quickly gaining in popularity due to their scalability and self-organizing nature, forming the basis for building large-scale similarity search indexes at low cost. However, most of the numerous P2P search techniques proposed in recent years have focused on single-key retrieval. A good example is the Content Addressable Network (CAN), which is a distributed hash table abstraction over Cartesian space.
Our objective is to develop a distributed storage structure for similarity search in metric spaces that would scale up with (nearly) constant search time. The advantage of the metric space approach for data searching is its 'extensibility', allowing us to perform exact match, range, and similarity queries on any collection of metric objects. Since any vector space is covered by a metric space with an appropriate distance function (for example the Euclidean distance), even n-dimensional vector spaces are handled easily. Furthermore, there are numerous metric functions able to quantify similarity between complex objects, such as free text or multi-media object features that are very difficult to manage. For example, consider the edit distance defined for sequences and trees, the Hausdorff distance applied for comparing shapes, or the Jacard coefficient, which is often used to assess the similarity of sets. Much research is now focused on developing techniques to structure collections of metric objects so that search requests can be performed efficiently.
A convenient way to assess similarity between two objects is to apply metric functions to decide the closeness of objects as a distance, which can be seen as a measure of the objects 'dis-similarity'. For any distinct metric objects x, y, z, the distance must satisfy the properties of reflexivity, d(x,x) = 0, strict positiveness, d(x,y) > 0, symmetry, d(x,y) = d(y,x), and triangle inequality, d(x, y) &Mac178; d(x, z) + d(z, y).
The distributed environment is composed of network nodes (peers), which hold metric objects, execute similarity queries on stored data and communicate with other peers. Every peer is uniquely denoted by its identifier PID. Peers hold data in a set of buckets. Each bucket has a unique identifier within a peer, designated as BID. Each peer also maintains a tree structure called the address search tree (AST). This is used to route similarity range queries through the distributed network. AST is based on the metric data partitioning principle known in the literature as the Generalized Hyperplane Tree (GHT). GHT is a binary tree with metric objects stored in leaf nodes implemented as buckets of fixed capacity. Inner tree nodes contain selected pairs of objects called pivots. Respecting the metric, the objects closer to the first pivot appear in the left subtree and those closer to the second are in the right subtree.
We start by building a tree with only one root node represented by a bucket B0 When the bucket B0 is full we must split it: we create a new empty bucket B1 and move some objects (half of them if possible) into it to gain space in B0. See Figure 1. The split is done by choosing a pair of pivots p1 and p2 from B0 and moving into bucket B1 all objects o that satisfy the condition d(p1, o) > d(p2, o).
 |
| Figure 1: Split of a GHT bucket. |
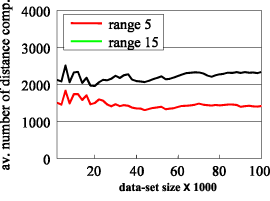
Pivots p1 and p2 are associated with a new root node and thus the tree grows one level. This split algorithm can be applied on any leaf node and is an autonomous operation (no other tree nodes need to be modified).
The most important advantage of GHT* with respect to single-site access structures is its scalability through parallelism. As the size of a data-set grows, new server nodes are plugged in and both their storage and the computing capacity are exploited. Figure 2 shows the result of the parallel response time of a range query, determined as the maximum of the costs incurred on servers involved in the query plus the search costs of the AST. For evaluation purposes, we use the number of distance computations (both in the AST and in all the accessed buckets) as the computational costs of a query execution. This experiment shows how the parallel search time becomes practically constant for arbitrary data volume and the larger the dataset the higher the potential for interquery parallelism. This is the most important feature of GHT*.
 |
| Figure 2: Parallel response time of a range query. |
Our future work will concentrate on strategies for updates (object deletion) and pre-splitting policies, plus more sophisticated mechanisms for organizing buckets.
Please contact:
Claudio Gennaro, ISTI-CNR, Italy
Tel: +39 050 315 2888
E-mail: claudio.gennaro isti.cnr.it
|
