Better Weather Forecasts with Use of Conservation Laws

by Jason Frank

Research at CWI aims to ensure structure in the midst of chaos. In long-time simulations of weather and climate, the Hamiltonian Particle Mesh method preserves Hamiltonian structure, and thereby energy, mass and vorticity. This technique could provide better quality solutions for weather forecasts.

Chaos was identified in meteorological systems in the 1960s by E.N. Lorenz. All solution curves of Lorenz's equations eventually become confined to a bounded region of space, yet two different solutions with only slightly perturbed initial conditions diverge from one another at an exponential rate. This divergence has dire consequences for any attempt to simulate the weather or climate with a computer, since errors that are necessarily made in the process of representing the original, analytical model in discrete form may be seen as perturbations of the solution. These unavoidable errors will, under the influence of chaos, cause the simulated solution to diverge from the true solution exponentially. With current numerical weather prediction technology, model and observation errors overwhelm the solution in roughly ten days.

On the other hand, the errors incurred in a numerical computer simulation are not random but systematic, taking the form of phase errors, numerical damping and so forth. For well-designed methods, the simulated solution may, while diverging exponentially from the true trajectory, still remain close to or 'shadow' some other solution satisfying a modified initial state, modified parameters, or even a perturbed model. In such cases, the solution may still be meaningful when properly interpreted. In other words, one may still be accurately simulating some weather; it is just unlikely that it will be the actual observed weather.

To deal with chaos, modern predictions of weather and climate often utilize an ensemble of simulations: a whole series of runs in each of which the initial state of the system is slightly perturbed. This yields a distribution of weather scenarios that can be subjected to statistical methods, and allows one to make statements like: "In 73% of all trials, rain was predicted for Amsterdam next Thursday".

When carrying out simulations on long-time intervals in which the numerical map is iterated, say, a hundred thousand to a hundred million times, the qualitative differences between algorithms become amplified. It is therefore crucial to employ methods having properties similar to those of the physical model being simulated (such as energy and mass conservation) or having similar mathematical structure (such as symmetries).

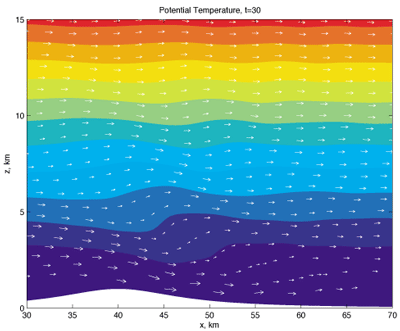
Research at CWI, in collaboration with Potsdam University, focuses on preservation of Hamiltonian structure in simulations of atmospheric models. Hamiltonian structure lies at the root of classical mechanical systems, and can be used to unveil many of the conservation laws present in such systems. Since viscosity can be neglected in large-scale atmospheric flows, the equations of motion are conservative, and from the Hamiltonian structure one can derive conservation laws of mass, energy and vorticity. By ensuring that the computational algorithm also adheres to this structure we can automatically guarantee that these conservation laws will also be inherited by the simulated solution. The preservation of Hamiltonian structure also has important implications for ensemble simulations. One can think of an ensemble of initial conditions as a set of points in space, each tracing out a solution. Initially the points are close together: for example, they form a ball. The ball is stretched and deformed as each point follows its solution trajectory. However, for Hamiltonian systems, the volume of the ball remains constant. This property is also inherited by the numerical method, and ensures that the members of an ensemble of simulations will each explore different possible scenarios, as opposed to being contracted to a smaller number of extremal solutions.

Preserving Hamiltonian structure using standard, purely grid-based computational techniques is difficult if not impossible. Instead we follow an approach in which a fluid is represented by a finite number of particles representing fluid masses, which satisfy classical mechanical equations of motion. For computational expediency, the potential field in which the particles move is represented on a grid. This is all carefully formulated to preserve Hamiltonian structure. The result is the Hamiltonian Particle-Mesh (HPM) method.

The HPM method has been under development since 2001. It has been used successfully for rotating planar and spherical shallow water equations, two-layer flows, and most recently, 2D vertical non-hydrostatic flow over topography. Figure 1 shows a simulation of a 2D non-hydrostatic flow over a mountain ridge using the HPM method, with the wind field (arrows) and potential temperature (color contours) indicated. Interest in non-hydrostatic models has grown in recent years as increased computational power has allowed higher grid resolutions to be attained. Current plans in this project address the issues surrounding 3D simulations.

Links:
http://www.cwi.nl/projects/gi/HPM/
http://www.cwi.nl/~jason/

Please contact:
Jason E. Frank, CWI, The Netherlands
Tel: +31 20 592 4096
E-mail: jasoncwi.nl