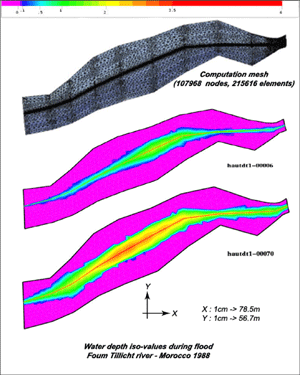
| |
Numerical Modelling and Analysis of Water Free Surface Flows
by Fadi El Dabaghi
A number of environmental engineering applications related to water resources involve unsteady free surface flows. A full three-dimensional model based on Navier-Stokes equations can give good descriptions of the physical features of certain phenomena, including lake eutrophication, transport of pollutants, floods and watersheds. However these models are characterized by significant computational cost. We aim to reduce this through the use of two-dimensional models or appropriate coupling models of different dimensions.
The models developed in this context can be classified into two categories: a two-phase flow model based on Navier-Stokes equations, and a shallow-water flow model.
Two-phase flow models have been used to simulate the remedial aeration used to combat eutrophication effects in lakes. A water reservoir is generally considered eutrophized when the concentration of dissolved oxygen drops below 3 mg/L. The idea behind remedial aeration is to inject compressed air into the bottom of the reservoir in order to stir up and oxygenate the water. The numerical simulation of the resulting flow by conventional models such as the two-fluids or Lagrangian models leads to many difficulties. This is mainly due to the models' complexity and the need for a fine grid in order to achieve a good representation of the effect of the bubbles.
These difficulties limit interest in these classical models and lead us to suggest some cheap and realistic alternatives. We consider a one-phase flow model based on velocity-pressure semi-compressible Navier-Stokes equations. Here, bubble dynamics are taken into account, firstly through boundary conditions related to the air injection velocity at the aerator position, and secondly by introducing correction terms representing the forces applied by the bubbles to the water. In the same framework, a more general two-fluids (air/water) model with a moving water free surface has been developed. We use realistic assumptions regarding the wind velocity and the atmospheric pressure with a convection equation describing the void fraction function of the water, which determines the wet domain. This allows us to treat the free surface effects of the lake in a more suitable manner, and consequently improve the dynamic results of the bubbles' aeration effects.
The second category of model is the shallow-water model: these describe river flooding, tidal fluctuations, bay and estuary flows, breaking waves on shallow beaches etc. They are derived from 3D incompressible Navier-Stokes equations by depth-averaging of the continuum mass and momentum balances. These models, known also as Saint-Venant, involve fluid-domain geometries characterized by their complexity and variability, and the large-scale computational aspects and fine grid necessary for realistic simulations.
To overcome these problems, we have used a priori and a posteriori error analysis. Geometric error indicators have been derived to improve the numerical simulations models by adaptive mesh techniques; these ensure an optimal quality solution at a required precision for a given computational cost. Moreover, the error indicators accurately predict in which parts of the fluid domain the flow model may be considered 1D, 2D or 3D, and can couple the resulting multi-dimensional models. In addition, we have integrated a conceptual hydrological model based on the HEC-HMS: this model computes run-off volume by subtracting the volume of water that is intercepted, infiltrated, stored, evaporated, or transpired from the precipitation in the catchment area. The result of this step, a flood hydrogram, forms the boundary conditions for the numerical models presented above (St-Venant) in simulating the flood.
 |
| Water depth iso-values during flood. Foum Tillicht river, Morocco 1988. |
|
From the numerical point of view, the approximation of the models mentioned above is based on the characteristics method for the time discretization of the advection terms. This method leads to an upwind scheme, which has the double advantage of being physically closed to convection, and being an explicit scheme unconditionally stable in the finite element context, thereby allowing the use of large and reasonable time steps. At each time level, we have to solve a quasi-Stokes problem, approximated by P1/P1 mixed finite elements for the velocity-height St-Venant formulation, or by (P1 + bubble /P1) mixed finite elements for the velocity-pressure Navier-Stokes formulation. This ensures the discrete LBB condition necessary in this context. For both formulations, the a priori error estimates are verified numerically on many academic test cases before the models are validated on real cases such rivers in flood or crossed 2D lake sections. Moreover, given that the real-time and large-scale computing requirements are very important for this kind of simulation, we used the HPCN facilities; this permitted the execution of developed codes, particularly on real test cases requiring finer and more complex meshes.
This work was supported by many Euro-Mediterranean projects (WADI , ESIMEAU and CruCID) and French bilateral cooperation programmes (CMIFM , CMEP and PLATON ). The EU projects were managed by ERCIM through a partnership constituted by INRIA-France, FORTH/IACM-Greece, EMI/ONEP-Morocco, ENP-Algeria, ENIT-Tunisia, RIKS-Holland, Calabria University-Italy and ESIB/CREEN/EUCLID-Lebanon.
Please contact:
Fadi El Dabaghi, INRIA, France
Tel:+33 1 3963 5343.
E-mail: fadi.el_dabaghi inria.fr
|
