Inference for Random Sets

by Marie-Colette van Lieshout

Image analysis and spatial statistics are widely used in medical diagnostics (eg body scans), satellite technology (eg cartography) and analysis of spatial correlation (eg in forestry and epidemiology). At CWI, scientists in the group Signals and Images have studied the problem of extracting linear features such as road networks from remotely sensed images. A new set of methods has been constructed based on Monte Carlo Markov Chain simulation. The corresponding new simulation procedures are faster and more precise than earlier methods.

Many images found in microscopy, material science and biology can be described as a set of independent, randomly placed particles. Think for example of the distribution of pine trees in a forest or, more aggressively, the distribution of fallen bombs. A formal description of such a random set is called a Boolean model. Notwithstanding the strong independence assumptions, inference is not trivial because of the occlusion effect: Only an image of all the particles - rather than individual particles is observable.

However, due to interaction, not all images can be described as completely random spatial patterns. Examples are the distribution of cells in the cat retina (eyes), metal particles in an alloy, and road networks. Cats' eye cells arrange themselves in two lattices, hard particles cannot penetrate each other and roads tend to be long and straight and have perpendicular crossings. Therefore, a class of more realistic models was studied, which permitted correlation between the particles: Gibbs random set models, which are defined by a parametric density, quantifying the interaction structure. The goals of CWI's research were to investigate the maximum likelihood estimation of these models, to devise efficient and exact techniques for them, and to develop useful models for image analysis practice.

For the latter goal, CWI researched the practical problem of extracting linear features - such as road networks - from remotely sensed images, in collaboration with the Ariana research team at INRIA. They had previously introduced the so-called Candy model, a Gibbs model for random sets consisting of line segments. In contrast to the Boolean model, there is interaction between the segments in the sense that configurations in which the segments tend to be aligned or cross at angles of about 90 degrees are favoured over patterns with many short, isolated segments or with an abundance of sharp crossings.

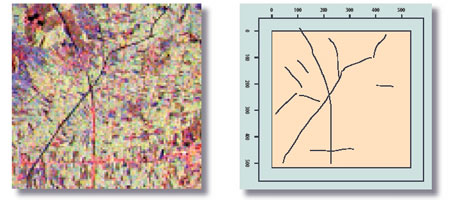Countryside region in Malaysia and extracted road map (Pictures: NASA (left) and CWI (right)).

Analysis of the interaction structure was used to define an efficient simulation algorithm. In this method the maximum likelihood estimation of the model parameters was carried out, and its uniqueness, consistency and asymptotic normality was established. The ideas were tested on publicly released satellite images obtained from the NASA/JPL website. An example is presented in the figures which show a rural region in Malaysia (left) and the extracted road network (right).

Various perfect simulation algorithms were also generalized to the random sets context and their relative efficiency was investigated for a range of random set models including the Candy model. Most perfect algorithms are based on well-known Monte Carlo samplers. For example, coupling from the past (CFTP) exhibits the dynamics of a spatial birth-and-death process, like the 'Life' simulator. It is particularly effective when the sampled distribution possesses some partial order structure. However, it generates a lot of objects that have no effect on the final outcome. In contrast, the clan of ancestors (ANCS) method aims to avoid births of objects that do not matter in the end, but does not take any model structure into account other than the range of interaction. It turns out that both methods take longer if the interaction strength increases, and that the ANCS method is more sensitive to the interaction range than CFTP.

Finally, a new method was proposed that for the first time allows the use of change moves that alter a single feature of the random set, a crucial step in using exact simulation in image analysis practice. A C++ library that incorporates all the above mentioned models and algorithms has been constructed.

Link:
http://www.cwi.nl/pna4
http://db.cwi.nl/projecten/project.php4?prjnr=125

Please contact:
Marie-Colette van Lieshout, CWI
Tel: +31 20 592 4008
E-mail: Marie-Colette.van.Lieshout@cwi.nl