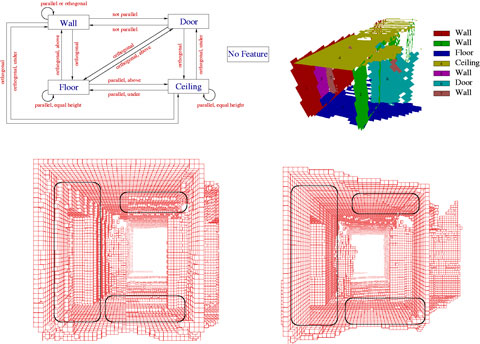
Kurt3D - An Autonomous Mobile Robot for Modelling the World in 3D

by Hartmut Surmann, Andreas Nuechter, Kai Lingemann and Joachim Hertzberg

Kurt3D is an autonomous mobile robot equipped with a reliable and precise 3D laser scanner that digitalizes environments. High quality geometric 3D maps with semantic information are automatically generated after the exploration by the robot.

Precise digital 3D models of indoor environments are needed in several applications, eg, facility management, architecture, rescue and inspection robotics. Autonomous mobile robots equipped with a 3D laser range finder are well suited for gaging the 3D data. We have equipped the autonomous mobile robot KURT2 and a mobile 3D laser range finder for the automatic generation of compact and precise 3D models. The proposed method consists of four steps.

First we use an autonomous mobile robot for gaging in 3D the environment. We use the mobile robot KURT2 and the AIS 3D laser range finder that is built on the basis of a 2D range finder by extension with a mount and a servomotor. The 2D laser range finder is attached to the mount for being rotated. The rotation axis is horizontal. Due to odometry errors, the robot's self localization is an unprecise measurement and therefore can only be used as a starting point for registration of the 3D scans in a common coordinate system. We have developed a very fast registration algorithm which extends the well known ICP (Iterative Closest Point) algorithm and aligned scans in less than 2 seconds.

Second we extract features, ie, planes from registered unmeshed range data. After the 3D scans are acquired we detect planar surfaces in the registered point cloud. No prior meshing algorithms need to be applied. Our algorithm is a mixture of the RANSAC (Random Sample Consensus) and the ICP algorithm. To detect a surface the algorithm randomly selects a point and estimates a plane through two neighbored data points. An ICP based optimization is started, if more than a certain number of data points exist in an epsilon area spanned by the estimated plane. Data points form the model set and their projections to the plane to form the data set for each iteration of the ICP algorithm. The plane is aligned given the measured data within a few iterations. The time-consuming search within the ICP algorithm is replaced by direct calculation of the closest point and the transformation is efficiently calculated by the use of quaternions. The extracted 3D planes are unbounded in size. Surfaces are finally extracted from the points by mapping them onto the planes. A quadtree based method generates the surfaces.

Third the computed planes are labeled based on their relative orientation. These scene interpretation uses the found features, ie, the planes. The background for interpretation comprises generic architectural knowledge. A model of an indoor scene is implemented as a semantic net. Nodes of a semantic net represent entities of the world/model. The relationship between the entities are encoded using different connections. Possible labels of the nodes are Wall, Floor, Ceiling, Door, NoFeature. The relationships between the features are parallel, orthogonal, above, under, equal height. The labels above and under are relative to their plane and hence not commutative. A depth first search (backtracking) is implemented to assign the labels to the set of planes according to the constraints in the semantic net. The computational expense is reduced by backtracking pruning and reusing (caching) of constraint tests.

Fourth we have implemented a knowledge based approach for the automatic model refinement. The merging of the views as well as the scanning process itself produces noisy data. Due to unprecise measurements or registration errors, the 3D data might be erroneous. These errors lead to inaccurate 3D models. The semantic interpretation enables the software to automatically refine the model. The planes are adjusted such that the planes explain the 3D data and the semantic constraints like parallelism or orthogonality are enforced. The main optimization process uses an error function to enforce the parallelism or orthogonality constraints. The error function consists of two parts. The first part accumulates the point to plane distances and the second part accumulates the angle differences given by the constraints. A suitable optimization algorithm for the the generated error function is Powell's method, because the optimal solution is close to the starting point. Powell's method finds search directions with a small number of error function evaluations. Gradient descent algorithms have difficulties, since no derivatives are available.

Figure 1: The autonomous mobile robot Kurt3D mapping a construction site.

The proposed methods have been tested in several experiments with our autonomous mobile robot Kurt3D in several environments eg Birlinghoven Castle and and various office corridors and hallways. The figure shows the reduction of the jitters at the floor and ceiling (circled). The orientation of the model in the bottom image is transformed along the axis of the coordinate system and the meshing algorithm produces flat walls. This transformation is done by using the semantic interpretation. It is not necessary to transform the model interactively into a global coordinate system or to stay in the coordinates given by the first 3D scan.

Figure 2: Top left: The semantic net used for the interpretation. Top right: A typical scene (corridor) with extracted labeled planes. Bottom: unconstrained and constrained mesh.

Future work will concentrate on the aspect of integrating camera images and enhancing the semantic interpretation by fusing color images with range data. The aperture angle of the camera will be enlarged using a pan and tilt unit to acquire color information for all measured range points. Furthermore we plan to concentrate on generating high-level descriptions and semantic maps including the 3D information, eg, in XML format. The semantic maps contain spatial 3D data with descriptions and labels.

Links:
http://www.ais.fraunhofer.de/ARC/3D/
http://www.ais.fraunhofer.de/ARC/kurt3D/

Please contact:
Hartmut Surmann, Fraunhofer AIS
Tel: +49 2241 14 25 18
E-mail: hartmut.surmann@ais.fraunhofer.de