Control Algorithms for Electroelastic Damping
by Maurizio Brocato and Evgeny Dudnikov
External fields may affect the mechanical properties of certain materials, which can thus be used in control devices. In the design of such devices, a control algorithm for a distributed parameter system must be used. We report here on options available during the development of an electrorheologic actuator at IEI-CNR.
The mechanical behaviour of electrorheologic fluids depends on the electric field applied. Sensors and actuators can be designed taking advantage of the properties of these fluids. The mathematical problem to be tackled is the control of a distributed parameters system, with the control acting on material elements in such a way that the parameters entering their constitutive description may be altered. The subcase we are studying is that of an elastic material with the elastic moduli depending, within limits, on the control field. The material can have varying degrees of stiffness as, for example, in an electrorheologic fluid undergoing small displacements, when an electric field is applied with varying intensity. The system under study can be controlled so that, although almost always elastic, its mechanical vibrations are damped. The damping is due to a transfer of mechanical energy into the energy of the controller (ie, in experiments in the high voltage generator). This is possible when, under imposed strain, the material changes from a stiffer to a softer state (see article in ERCIM NEWS 38).
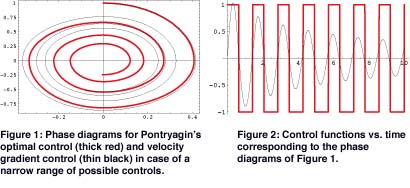
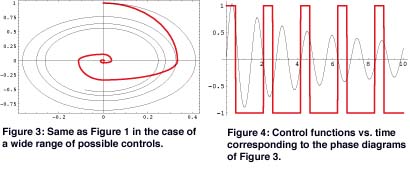
In a previous paper, the first author suggested the use of an extended Pontryagin’s Maximum Principle, applicable to distributed parameters systems. To find optimal damping, minimum total kinetic energy was sought. The resulting optimal paths are of the type shown with thick red lines in Figures 1 and 3, on a deformation vs. rate of deformation plane: maximum or minimum stiffness must be provided respectively when the elastic energy increases or decreases. The solution represented in Figure 1 differs from that of Figure 3 because the range within which the controlled stiffness varies is wider in the second case. The bang-bang type control functions, corresponding to the two above-mentioned solutions are shown vs. time, with thick red lines in Figures 2 and 4 respectively. This control strategy can be implemented through a feed-forward loop as follows: sense the velocity and compare it with the previous measurement; if the two samples have different signs, switch the electric field from off to on or vice versa.
If forced vibrations must be damped, the same strategy proves useful when no forcing frequency is lower than the lowest natural frequency of the system. Otherwise, more complex algorithms must be implemented.
Thus we have investigated the possibility of stabilizing the system through the method of velocity gradient developed by the group of A. Fradkov at St Petersburg. This method may be computationally easier to implement than Pontryagin’s. Three classes of solutions are generally provided: differential, linear and relay control. In our case, the latter corresponds to the bang-bang solution suggested by Pontryagin’s Principle. Application of the linear control algorithm to our example gives trajectories and control functions of the type shown with black thin lines in the figures. When the range of possible controls is relatively narrow, trajectories are close to the optimum, especially during the first few periods. The control function must then be updated. Feedback loops are thus required in applications.
This work was funded by a fellowship of the Italian Ministry of Foreign Affairs awarded through the Landau Network-Centro Volta.
Please contact:
Maurizio Brocato - IEI-CNR
Tel: +39 050 593 422
E-mail: brocato@iei.pi.cnr.it
