Process Systems: Theory and Applications from Different Aspects
by Katalin Hangos and Gábor Szederkényi
Combining a priori phyisical and engineering knowledge with theories of artificial intelligence, discrete event systems and modern nonlinear control has led to new theoretical results and successful applications in the field of modelling, analysis and control of process systems at the Process Control Research Group at SZTAKI.
A rough definition for process systems is that the operation of such systems is based on the laws of thermodynamics. Well-known examples of process systems include heat exchangers, chemical reactors, distillation columns and wastewater treatment systems. The Process Control Research Group is part of the Systems and Control Laboratory of SZTAKI, and studies the modelling, analysis and control of process systems.
Process Modelling and Model Analysis
Process models for control and diagnostic purposes most often take the form of differential-algebraic equations (DAEs), with the conservation balances being the differential part and the constitutive equations the algebraic part. A number of hidden relationships exist between the equations and their terms, as dictated by the laws of thermodynamics, unit operation, reaction kinetics, heat and mass transfer. Together with these relationships, the equations can be seen as structured texts (like computer programs) with a syntax and semantics defined implicitly by the underlying laws of thermodynamics and chemical engineering. This approach enables us to use formal methods of computer science to construct, verify, analyse and simplify process models in a rigorous and automated way. Our latest results in this field are an assumption-driven model-building procedure, a systematic model-simplification method and an assumption-retrieval procedure for the determination of simplification assumptions of two related process models. Furthermore, the prototype of an assumption-driven model editor has been developed in Prolog language. Cooperating partners in this research area are the Department of Computer Science at the University of Veszprém in Hungary and the Computer Aided Process Engineering Centre in the Department of Chemical Engineering at the University of Queensland in Australia. Several years of joint work resulted in a book entitled ’Process Modelling and Model Analysis’, written by Katalin Hangos and Ian Cameron and published by Academic Press in 2001.
Intelligent and Discrete Process Control
Intelligent and discrete process control and diagnostic methods apply so-called discrete event system models, which are currently one of the hottest research topics in systems and control theory. Such systems are widely found in practical applications and are characterised by the presence of discrete valued variables: state, input and output variables with a finite number of possible values. At present, our research in this field is focussed on the hierarchical decomposition and analysis of process models using hierarchical coloured Petri Nets. Our previous results on.the invariance inheritence in Petri Nets and the application of Artificial Intelligence methods in generating operating procedures serve as a starting point for this work. Recently, we successfully utilised hierarchical coloured Petri Nets for multiscale-modelling, deadlock-detection and fault diagnosis in an industrial granulator system. The simulation results run on the validated system model are promising, making the next short-term goal to implement the developed techniques on the real system.
In 2001, Kluwer Academic Publishers published a book in this field with the title ’Intelligent Control Systems (An Introduction with Examples)’, written by Katalin Hangos, Rozália Lakner and Miklós Gerzson
Nonlinear Process Control
Nonlinear system theory and the nonlinear control and diagnosis methods based thereon form one of the most challenging and fast-developing areas in modern systems and control theory. Its significance is explained by the fact that most engineering systems (and process systems in particular) show nonlinear behaviour, with a few exceptions of continuously operated systems near a well-defined and stable operation point.
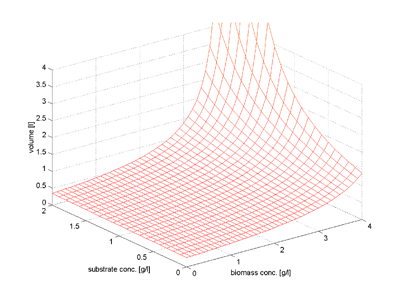 |
| Figure1: Reachability surface in the state space of a simple fed-batch fermentation process. |
Apart from its practical importance, nonlinear systems and control theory requires the understanding and application of advanced mathematical concepts and tools from the areas of nonlinear differential equations, functional analysis, differential manifolds and algebra and symbolic computations. It turns out, however, that the principles of the engineering discipline governing the behaviour of the nonlinear system play a key role in the understanding, analysis and control of engineering systems. Thus the use of engineering knowledge determines certain structural properties of a nonlinear system, and this can make it feasible or even easy to handle otherwise very difficult problems. This type of interdisciplinary approach to control problems is commonly called a ’grey-box’ approach. Recent research results show that this approach can be successfully applied for the nonlinear analysis of control-related features such as local and global stability, reachability, observability, passivity and zero dynamics. These analysis results together with physical and engineering knowledge allow us to understand the dynamic behaviour of process systems in more depth, and to select and design nonlinear controller structures with the properties we require.
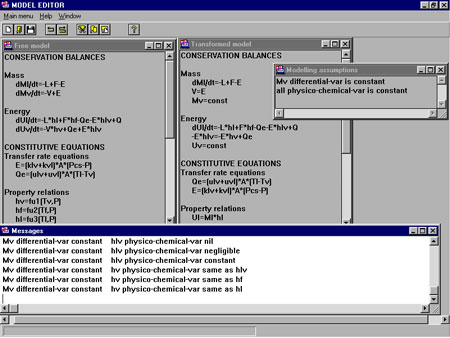 |
| Figure 2: Screenshot from the assumption-driven model editor software (analysis of model transformations). |
In the field of nonlinear mechanical systems, the Hamiltonian description of these systems gives rise to their special characterisation and the development of their very powerful passivity-based control. The analogy with the Hamiltonian description of mechanical systems has led to the Hamiltonian description of process systems.
The developed methods were successfully tested on a variety of process systems:
- fermentation processes with highly nonlinear reaction kinetics operated in continuous or fed-batch mode
- a low-power nonlinear gas-turbine (in cooperation with the Department of Aircraft and Ships at the Budapest University of Technology and Economics and the János Bolyai Military Technical College Faculty of the Miklós Zrínyi National Defence University)
- a nonlinear electro-pneumatic valve within the brake system of trucks (in cooperation with the Research and Development Center of Knorr-Bremse Brake-systems Ltd. in Budapest).
Our most important partner in this area of activity is the Systems and Control Laboratory of SZTAKI, and a significant result of this cooperation is another book, entitled ’Analysis and Control of Nonlinear Process Systems’ and written by Katalin Hangos, József Bokor and Gábor Szederkényi, which is to be published by Springer-Verlag in early 2004.
Links:
http://www.sztaki.hu/scl
http://daedalus.scl.sztaki.hu
Please contact:
Katalin Hangos, SZTAKI
Tel: +36 1 279 6101
E-mail: hangos scl.sztaki.hu scl.sztaki.hu
|




