A Colourful Theory on Graphs

by Zsolt Tuza

The concept of List Colouring is a relatively new issue in the field of graph colouring theory. It is related to hot topics of applications, most notably the frequency assignment problem in wireless communication. In a somewhat different form, its study at SZTAKI dates back to the late 1980s when we encountered a practical scheduling problem. Since the mid-1990s we have carried out related work in active collaboration with researchers from several countries.

In the standard formulation of the List Colouring problem, a graph (network) and lists of colours allowed for its vertices (nodes) are given. The goal is to select one colour for each vertex from its list in such a way that adjacent vertices never get the same colour. An alternative approach, called Precolouring Extension, starts from a feasible colouring of a part of the graph in question, and asks for the minimum total number of colours admitting a colouring of the entire graph that extends the partial colouring given. A more general variant is the Set Colouring problem, where one has to select several colours for each vertex from its list. (The colours selected for adjacent vertices must be distinct.)

In this area we carry out research in various directions. A fundamental question is whether a given collection of lists admits any feasible colouring. One goal of our research is to draw a sharp line separating the efficiently (ie, polynomial-time) solvable problem instances from the intractable classes. Another interesting question is how much larger subsets can be selected if the lists of allowed colours are larger with a given amount. Particular types of graphs, eg planar networks, are of importance, too.

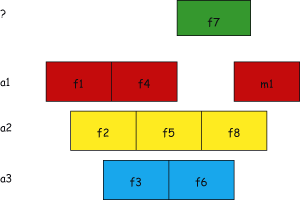
Figure 1: Greedy algorithm requires 4 colours.	Figure 2: A better solution with 3 colours.

In one of the applications the vertices represent transmitters, the list of colours allowed for a vertex contains the frequencies locally usable, and adjacency means that interference may occur between the corresponding two stations and hence they should not use the same frequency. In this interpretation, selecting large subsets of the colour lists ensures that the stations can operate on a fairly wide range of frequencies without the danger of interfering with each other.

In another application — what was the starting point of our research on Precolouring Extension — a mixed type of scheduling has to be found. Given a maintenance plan for a fleet of airplanes, and given the flights in the timetable, the problem is to assign the flights to the airplanes in such a way that the assignment be compatible with the maintenance plan. In this model the vertices represent time intervals (maintenances and flights), the colours correspond to the airplanes, the precoloured part is the set of maintenances, and adjacency means that two represented time intervals overlap.

In the paper where we initiated the study of Precolouring Extension with Miklós Biró and Mihály Hujter (both ex-SZTAKI), we designed an efficient algorithm that finds, in terms of the mixed aircraft scheduling problem, a feasible schedule whenever it exists, provided that each airplane has just one maintenance within the time horizon considered. In later works with Mihály Hujter we investigated the algorithmic complexity of the graph-theoretic problem under various conditions, and also studied related structural questions on some interesting particular classes of graphs. We have discovered good characterisations (efficiently testable necessary and sufficient conditions) for the extendability of partial colourings with a given number of colours.

We have explored the area of Set Colouring in joint research with Margit Voigt (TU-Ilmenau). With the collaboration of Noga Alon (Tel-Aviv University) we have proved that for sufficiently large lists of allowed colours it is precisely the graph invariant called ‘fractional chromatic number’ that expresses the proportion of colours that can be selected from each list. Moreover, in joint work with Jan Kratochvil (Charles University, Prague) we proved that this estimate, which is tight in general, can significantly be improved when stronger conditions hold for the pairs of adjacent lists.

The concepts described above have many interesting connections to other areas, too, with an extensive and continuously growing literature. (For an overview of results discovered until mid-1997, see Zs. Tuza: Graph colorings with local constraints — A survey, Discussiones Mathematicae Graph Theory, 17:2 (1997), 161–228.)

The area offers lots of challenging open theoretical questions as well. Among others, this includes problems on graphs where feasible colourings exists whenever the size of every list is at least as large as the ‘chromatic number’; and on the largest possible number of vertices in partial colourings if the lists are not large enough to make the entire graph colourable.

It has also turned out that List Colouring can be formulated as a subproblem of the Colourability problem of ‘mixed hypergraphs’, a concept introduced by Vitaly Voloshin (Academy of Sciences of Moldova, Kishinau) about a decade ago. In mixed hypergraphs, two types of sets are distinguished, and vertex colourings are to be found where each set of the first type has two vertices of the same colour, while each set of the second type has two vertices of distinct colours. We carry out research in this direction with Gábor Bacsó (SZTAKI) and Lorenzo Milazzo (University of Catania).

We are open to extend our broad international cooperation to further research centres of Europe, both in theory and applications.

Please contact:
Zsolt Tuza, SZTAKI
Tel: +36 1 297 6110
E-mail: tuza@sztaki.hu