Scalable Solvers for Sparse Linear Systems

A serious bottleneck in performing large-scale numerical simulations is the speed by which the underlying sparse systems of equations can be solved. In cooperation with commercial software providers, the Fraunhofer Institute SCAI attempts to increase the efficiency of the basic numerical solvers by introducing modern solver technology.

In various application fields such as fluid dynamics and structural analysis, industry is increasingly relying on computer simulations. The physical structures to be analyzed on the computer are discretized by means of complex grids. The finer the resolution of these grids, the higher the accuracy of the corresponding numerical simulation. Unfortunately, however, increasing the grid resolution also increases the size of the corresponding (sparse) systems of equations which have to be solved numerically. Problems with many millions of degrees of freedom (unknowns) are being tackled nowadays and grid sizes will substantially grow further in the near future. The resulting large systems of equations can no longer be solved efficiently with standard numerical approaches such as conjugate gradient combined with classical preconditioners. Instead, hierarchically operating solvers are required.

The classical multigrid or multilevel approach, representing one of the major work areas of SCAI, was the first hierarchical approach to reach maturity. Rather than operating merely on the given (very fine) grid, corresponding methods combine the numerical information resulting from a (pre-defined) hierarchy of increasingly coarse grids. Compared to classical one-level solvers, the main advantage of properly designed multilevel approaches is their numerical scalability. That is, the computational work to solve the underlying systems of equations grows only proportionally with the number of unknowns. Depending on the concrete application, the computational gain may be enormous, and it increases further with increasing problem size.

Unfortunately, the integration of classical multigrid approaches into existing commercial simulation software is usually not feasible. One reason is that commercial software typically has been developed over a period of many years and the underlying data structure has not been designed with the special requirements of multigrid approaches in mind. Moreover, industrially relevant grid models are often so complex that the explicit construction of a ‘natural’ hierarchy of grids, as required by a classical multigrid method, is very complicated if possible at all.

Thus, a focus of the work at SCAI is on the development of ‘algebraic’ multigrid approaches (AMG). Corresponding solvers attempt to combine the advantages of classical multigrid approaches with those of easy-to-use plug-in solvers. To be more specific, in contrast to classical ‘geometric’ approaches which operate on a geometrically pre-defined hierarchy of grid levels, AMG directly operates on the linear matrix problem which corresponds to the finest-level discretization. The explicit construction of a reasonable multilevel hierarchy is part of the AMG algorithm (invisible to the user of AMG), automatically performed by exploiting algebraic properties which are easily accessible through the discretization matrix such as sign and size of entries. That is, only the discretization matrix and right hand side have to be passed to an AMG solver making it as easy to plug into an existing simulation code as any standard one-level solver. This makes AMG solvers particularly interesting for an integration into existing commercial simulation packages.

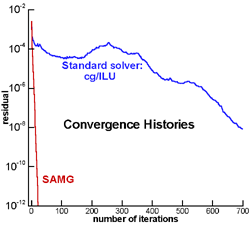
A major result of the AMG development at SCAI is an advanced solver package, SAMG, which is continuously being enhanced and extended to cover more and more applications. SAMG is most mature for discretized scalar elliptic partial differential problems as arising, for instance, in computational fluid dynamics, oil reservoir simulation, ground water flow and circuit simulation. As an example, Figure 1 compares the convergence history of SAMG with that of a standard one-level solver. Here, the underlying application is the solution of a single pressure equation arising in a reservoir simulation on a grid consisting of 1.16 million cells. Compared to the standard solver, the total computational time is reduced by nearly a factor of 20. This factor will grow further with increasing grid size. For discretized systems of partial differential equations, major research still has to be performed. However, substantial progress has been achieved in various application areas such as linear elasticity and semiconductor process- and device-simulation (see Figure 3).


Figure 1: Example from oil reservoir simulation: Convergence history of SAMG versus that of a standard solver.	Figure 2: Parallel performance of SAMG for the same example as in Figure 1.

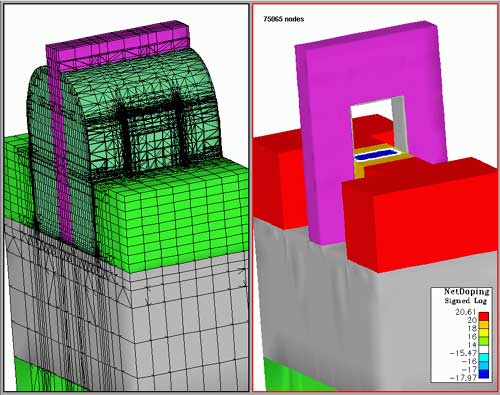
Figure 3: FinFet transistor and underlying grid used for performing a device simulation (courtesy of Avant).

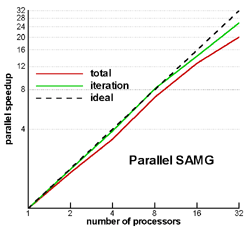
Further progress in numerical simulation requires the effective combination of advances in both computer and algorithm development. Ultimately, the best of all known (sequential) algorithms need to be considered for efficient parallelization. Due to their numerical scalability, hierarchical methods play an outstanding role. Consequently, a parallel version of SAMG has been developed (based on a distributed memory programming model). It can be applied to any reasonable partitioning of the given grid. Parallel SAMG scales very well as long as the number of mesh cells per processor is some 30,000 or more. Clearly, given a number of processors, the larger the grid, the higher the parallel efficiency. For the above case of 1.16 million cells, the measured speedup on 32 processors is 26 for the (iterative) solution phase, and 20 for the complete run, including SAMG’s preparational phase in which the hierarchy is constructed (see Figure 2).

Please contact:
Klaus Stüben, Fraunhofer-SCAI
Tel: +49 2241 14 2749
E-mail: klaus.stueben@scai.fhg.de