Shape Geometry and Aesthetics

by Franca Giannini and Marina Monti

FIORES-II is a research project of the European Commission that aims at investigating and identifying the links between emotional shape perception and geometry, in order to facilitate communication between designers and CAD operators and to create more user friendly tools for aesthetic design.

The market success of industrial products strongly depends on their aesthetic character, ie the emotional reaction that the product is able to evoke. To achieve their aim designers have to act on specific shape properties, but at present they are not directly supported in this by existing digital tools for model definition and manipulation, mainly because of the still missing mathematical formalisation of the properties themselves. The European project FIORES-II (GRD1-1999-10785-Character Preservation and Modelling in Aesthetic and Engineering Design), started in April 2000, aims at investigating and identifying the links between emotional shape perception and geometry and to create, through their mathematical formalization, more user friendly tools for aesthetic design

Relationships Between a Physical Form and its Emotional Message
In order to develop modelling tools to allow designers to quickly attain the desired emotional message, it is necessary to understand the procedures they follow to achieve their objectives. Within the FIORES-II project, design activities in different industrial fields have been analysed in depth and the language used in different phases of the design cycle has been studied. It emerged that the terms strictly related to emotional values (eg dynamic, aggressive, etc.) that express the objectives to be achieved by the end product are mainly used when designers talk with marketing people. On the other hand, during the creation and modification of the digital model, designers communicate their aesthetic intent using a more detailed and restricted set of terms corresponding to shape properties. In this phase they provide instructions on which elements and properties have to be changed to realise their objective (eg making a curve a bit more accelerated, or decreasing the tension of … ) and to fulfil marketing directives. This second set of terms represents the first link between low-level geometric properties and the high-level features of a product. Therefore, in order to identify links between message and geometric shape, we envisage a two-level mapping: the first level links geometric properties to design terms; the second links these latter to the emotional message.

Starting from the above considerations, major attention has been given to mathematically formalising the most used terms of the Language of the Trade (ie Acceleration, Tension, Convexity, Concavity, Lead in, Crispness, Sharpness, Softness, Crown), with the objective to develop modelling tools which are fundamental for:

• direct shape modification with a stronger semantic control than that offered by classical methods
• specification of the aesthetic properties in objective terms
• aesthetic feature modification.

The development of these tools implies the solution of the following problems for each term:

• definition of its meaning from the design viewpoint: what shape does the designer expect when the modifier value changes for the entity considered? Which geometric properties are affected by the modifier?
  
• specification of the mathematical function producing the expected shape modification and the related application domain
• identification of the parameters to be provided by the user or specified automatically for character preservation, plus the specification of which parameters can be used within an optimisation process, and how
• evaluation metrics for the modifier for testing purposes.

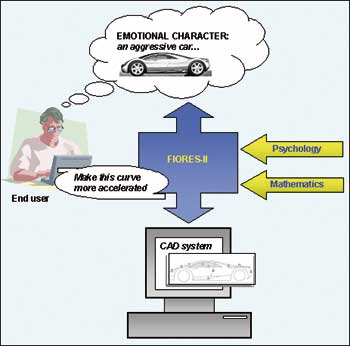The FIORES-II framework.

As an example, to illustrate how the above points have been mathematically solved, the convexity property is briefly described. Traditionally a curve is convex/concave, if the curvature (ie the second derivative) along the curve has the same sign. In our case, it has a more specific meaning. Interviews with the end-users reveal that judging a curve as more or less convex depends on several factors: symmetry, roundness, curvature variation…. Many of these factors depend in turn on mathematical properties that can be calculated on the curve and have to be combined to define a suitable measure criterion, which has to be continuous and differentiable. We took into account the aspects that are implicitly judged by the users, as well as mathematical properties such as curve length, area enclosed by the curve, coordinates of the gravity centre, momentum of inertia of the lamina with respect to the axes of the local coordinate system along the curve, etc. The combination of these properties (by means of the Minkowsky measure and with the adoption of weights for better calibration) provided a measuring criterion corresponding to the user feedback in a quite satisfying way.

The theoretical specification of the tools is almost complete and the implementation of a software prototype is currently under development.

It has not been easy to acquire a full understanding of how designers perceive shape and then to translate this into mathematical formalism. Even if some of the terms used have a direct mathematical counterpart, the meaning is not always the same. For example, not all curves in which the second order derivative increases are necessarily perceived as accelerating curves. Moreover, different shapes may be perceived as having the same property value. This means that several variables contribute to a single property, thus requiring a further level of interpretation to give a formal description of their interdependencies.

The preliminary results confirm the validity of the approach not only from the point of view of user interest but also from a scientific perspective, linking different disciplines such as mathematics and perceptual psychology.

Link:
Project home page: http://www.fiores.com

Please contact:
Franca Giannini, IMATI-CNR
Tel: +39 010 6475666
E-mail: giannini@ima.ge.cnr.it