Algebraic Convergence of Pulled Fronts

Propagating fronts which separate regions of different behaviour are quite common in Nature. A particular situation arises if the state ahead of the front is linearly unstable, like in the spreading of an epidemic. Recently researchers at CWI and Leiden University isolated the universal part in the expression for the speed of such fronts. Their results bear on several nonlinear phenomena including gas discharges.

Examples of fronts penetrating into an unstable state range from the expansion of bacterial colonies to the branching of electric discharges. The mother of all equations describing such phenomena is a nonlinear reaction-diffusion partial differential equation called the Fisher-Kolmogorov equation, originally designed in the 1930s to describe epidemics:

The state u = 0 can be shown to be unstable, ie, a small disturbance can very quickly grow out to substantial size. The state characterized by u = 1 turns out to be stable. If the system was initially in the state u = 0, a wave front between these two states propagates with a certain, time-dependent velocity v, whose asymptotic expansion for large times is given by:

v(t) = a + b / t + c / t ^3/2 + O(1 / t ²)

where a, b and c are numerical constants (equal to 2, -3/2, and 3

/2, respectively). Note that the leading correction terms for large, but finite times are algebraic, not exponential (as it would be for fronts propagating into a metastable rather than an unstable state). The universal term ~1/t was derived by Bramson (1983) in a lengthy paper. Using asymptotic expansions and resummations, U. Ebert and W. van Saarloos recently determined the next order universal term ~1/t3/2 (the time-dependent shape of the wave front). Moreover, they showed that the higher order terms O(1/t²) are not universal, but depend on details of the initial conditions. They also derived a simple universal expression for the convergence of the front profile. Amazingly, their method can also be applied to many other equations, including those with more complicated differential operators (eg, the Swift-Hohenberg equation), certain integro-differential equations, coupled sets of reaction-diffusion equations, and the equations describing an electric discharge. In all these cases the velocity v(t) of the ‘pulled’ wave front is given by the above expression, only with different equation-specific numerical constants. The front is called a ‘pulled’ wave front because it seems that there is a leading edge pulling along the full front with all its complex system-dependent structure, with an almost universal speed. This is the result of a new ‘center manifold theorem’ for the expansion about the asymptotic solution: in the limit of large times, not the full equation is relevant, but only a restricted mathematical substructure that can be identified by a saddle-point expansion of the linearized equation. However, although the analysis of the linearized equation plays a central role in the calculation, the convergence law differs quantitatively from that of the linearized equation. Wave fronts with such an algebraically slow relaxation pose various problems to analytical perturbation theory and to numerical schemes with local refinement. Both are presently under investigation at CWI.

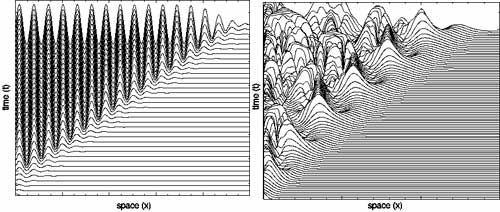Two examples of fronts propagating into an unstable state. The dynamics are shown by plotting the fronts one above the other at successive moments. The front on the left gives rise to a periodic state, the one the right creates a chaotic state. Nevertheless, the way in which these fronts ‘mature’ (ie approach their asymptotic speed and front shape) is given by one and the same formula.