MUMPS: A Multifrontal Massively Parallel Solver

The solution of large sparse linear systems lies at the heart of most calculations in computational science and engineering and is of increasing importance in computations in the financial and business sectors. Today, systems of equations with more than one million unknowns need to be solved. To solve such large systems in a reasonable time requires the use of powerful parallel computers. To date, only limited software for such systems has been generally available. The MUMPS software addresses this issue.

MUMPS was originally developed in the context of the PARASOL Project, which was an ESPRIT IV Long Term Research Project for developing ‘An Integrated Environment for Parallel Sparse Matrix Solvers’. The Project started in January 1996 and finished in June 1999 and a version of MUMPS was publicly released in March 2000. An important aspect of the PARASOL project was the strong link between the developers of the sparse solvers and the industrial end users, who provided a range of test problems and evaluated the solvers.

Since then MUMPS has continued as an ongoing research project and a new release of the package is imminent. It is the purpose of this article to describe recent work that has led to the new facilities available in this release.

The MUMPS package uses a multifrontal approach to factorize the matrix (Duff and Reid, The multifrontal solution of indefinite sparse symmetric linear systems, ACM TOMS, 9, 302-325). The principal feature of a multifrontal method is that the overall factorization is described (or driven) by an assembly tree (see Figure 1, left).

At each node in the tree, one or more variables are eliminated using steps of Gaussian elimination on a dense matrix, the frontal matrix.Each edge in the tree represents the movement of data of a child node to its parent (which is the adjacent node in the direction of the root). An important aspect of the assembly tree is that it only defines a partial order for the factorization. That is, arithmetic operations at a pair of nodes, where neither lies on a path from the other to a root node, are independent. For example, work can commence in parallel on all the leaf nodes of the tree. Operations at the other nodes in the tree can proceed as soon as the data is available from the children of the node. There is thus good scope for exploiting parallelism, especially since assembly trees for practical problems contain many thousands of nodes.

The efficiency of a direct solver is very dependent on the order in which the variables of the problem are eliminated. This largely determines the amount of work that is to be done during the factorization and hence the overall time for solution. Furthermore, the elimination order of the variables also determines the number of entries in the computed factors and the amount of storage required. In the earlier versions of MUMPS, the only in-house ordering supplied was the Approximate Minimum Degree (AMD) algorithm of Amestoy, Davis, and Duff (SIAM J Matrix Anal and Applics, 17, 886-905), but recent experiments have shown that while this ordering is usually best on discretizations from 2D problems, other orderings, particularly spectral based orderings and minimum fill-in orderings, can do better on larger problems from 3D discretizations. Thus, in the new version of MUMPS, we have included a wide range of ordering packages including PORD (Jürgen Schulze), SCOTCH (LaBRI, Bordeaux), and approximate minimum fill-in orderings. In a somewhat more loosely coupled way, orderings from the MeTiS package from Minneapolis can be used.

For nodes far from the root, to keep communication to a minimum while maintaining a high level of parallelism, MUMPS maps a complete subtree onto a single processor of the target machine (see Figure 1, right). The nodes near the root of the assembly tree normally involve more computation than nodes further away from the root. In practical examples, we observed that more than 75% of the computations are performed in the top three levels of the tree. Unfortunately, the number of independent nodes near the root is small, and so there is less parallelism to exploit. For example, the root in Figure 1 has only two neighbouring nodes and hence only two processors would perform the corresponding work while the other processors remain idle.

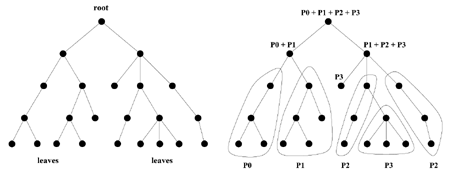Example assembly tree (left) and a possible distribution of the computation over four processors P0, P1, P2, and P3 (right).

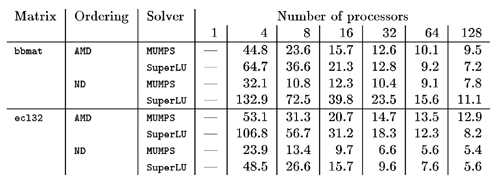Table: Factorization time (in seconds) of large test matrices on the CRAY T3E.
‘—’ indicates not enough memory.

It is thus necessary to obtain further parallelism within the nodes near the root by partitioning these nodes among several processors. In addition, because MUMPS is designed to solve a wide range of problems including symmetric and unsymmetric problems, numerical pivoting is performed within the numerical factorization. This means that only a static analysis of the sparsity pattern and a static allocation of tasks to processors could be very inefficient if significant numerical pivoting is required. We have chosen to deal with this through using dynamic allocation of tasks during the numerical factorization. This also has the benefit of enabling the code to perform well when we are not in a single-user environment. We have done much recent research on the best way of performing this allocation. In the earlier versions of MUMPS, the processor to which a computationally expensive node is assigned, partitions the corresponding frontal matrix, and distributes the parts dynamically over processors that have a relatively low load. The elimination operations on this frontal matrix are subsequently performed in parallel. In the new version, the number of candidates which can be chosen is restricted during the prior static analysis phase resulting in a dynamic allocation that is much more more efficient in both memory estimation and usage and execution time.

The original MUMPS package was only designed for real matrices but, in the new version, complex symmetric and complex unsymmetric systems are permitted. If there is sufficient demand, a version for complex Hermitian systems might be developed in the future. The MUMPS software is written in Fortran 90. It requires MPI for message passing and makes use of BLAS, LAPACK, BLACS, and ScaLAPACK subroutines. However, in recognition that some users prefer the C programming environment, a C interface has been developed for the new release, and a version has been written that avoids the use of MPI, BLACS, and ScaLAPACK. This would be suitable for running in a single processor environment, perhaps for testing and development purposes.

MUMPS has been ported to a wide range of computers including the top-line supercomputers from Compaq, Cray, IBM, and SGI and we are currently working on the efficient exploitation of multilevel parallelism and memory management, such as is present on the new IBM SP range of computers. The MUMPS package has a good performance relative to other parallel sparse solvers. For example, we see in Table 1 comparisons with the SuperLU code of Demmel and Li. These results are taken from ‘Analysis and comparison of two general sparse solvers for distributed memory computers’, ACM TOMS, 27, 388-421.

Link:
http://www.enseeiht.fr/apo/MUMPS/

Please contact:
Iain S Duff, CLRC
Tel: +44 1235 445803
E-mail: i.s.duff@rl.ac.uk