
|
|
ERCIM News No.46, July 2001 [contents]
|
by Gavin Doherty, Giorgio Faconti and Mieke Massink
TACIT is a research network addressing its research towards integration and unification concerns and the use of novel technologies for the support of continuous interaction techniques. The network includes as partners three members of ERCIM (CNUCE, RAL, FORTH) together with the German Institute for Artificial Intelligence (DFKI) and the Universities of Bath, Grenoble, Parma, Sheffield, and York.
Interactive systems in the modern world are becoming both increasingly pervasive, and increasingly rich in the variety of tasks supported, the amount of information available, and the different ways in which the user can interact with them. Interacting with such systems involves multiple media, supporting a continuous flow of information. The shift towards more continuous interaction means that important properties of such systems are better expressed in terms of some quality of service parameter with time playing a central role (latency and jitter are often critical to the usability of a system).
With this motivation, an approach to modelling is to apply timed specification and analysis techniques to encode a set of assumptions about user behaviour in a user model. Although human behaviour is inherently non-deterministic it can be expected to follow probability distributions, and so an interesting possibility is to apply stochastic techniques to consider uncertainty in user models.
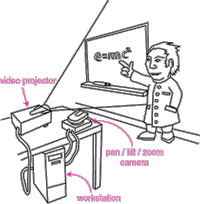
The following example illustrates how stochastic models may be used to represent both user and system behaviour. The example refers to the MagicBoard, an augmented reality interactive whiteboard based on a finger tracker and image projection, developed at the University of Grenoble (see figure 1).
What distinguishes this application from an electronic whiteboard is that the user draws directly on the board with real pens; what is drawn on the board is scanned by the system by means of a camera. The user uses gestures to select, copy, paste, etc. what is drawn on the board. The results of the operations are projected back on the board. Thus there is gestural input from user to system, and feedback both of the userís input (real ink on the board) and from the system (ëdigital inkí projected on the board). Userís gestures are captured by the system that recognise and track a userís finger. A cursor is displayed (by projection) on the board when the system is tracking and gives the user feedback about whether it is able to follow the position of the finger. We use the stochastic process algebra approach to model this aspect of the MagicBoard interface and examine the relation between system performance and the constraints placed on userís behaviour. The situation that we examine is one in which the users need to slow down their movement to allow the system to keep up.
In order to develop a model we make a number of assumptions about the real-time behaviour and its variability of both system and users. Part of the necessary information is obtained from the literature. In particular, the delay generated by the tracker is assumed to be modelled by an exponential distribution because each lag occurs independently from any previous lag (memoryless property).
The timing aspects related to the behaviour of the user are of a different nature. We need to know how much time it takes for users to move their finger from one point to another on the whiteboard in an unconstrained way. Further we need to know how much the movement slows down when the user observes a lag in feedback.
In order to have reasonable data for our illustration, we require data on the human performance for moving a finger over large distances and in different directions. We have available experimental data collected at the University Joseph Fourier in Grenoble, showing that the variability in time of fingers movement from one place to another on the whiteboard follows a lognormal distribution. Since the distances that are covered are relatively long, the initial part of the movement is performed very quickly; from the motor skills literature we take this as the initial ballistic part of the movement. The last part of the movement is performed more slowly and we take this as corresponding to the visually guided part of the movement to the target.
Following the (uninterruptible) ballistic part of the movement, the users check whether the cursor is managing to follow their finger. A delay may be introduced at this point before the final part of the movement. Finally, we must formulate our assumptions about the threshold of time for the user to take account of the lag (taken as cognitive delay) and the delay introduced by the user taken as a combination of cognitive and motor delay. For these delays we use the bounds data from a model of the human information processor. A similar argument holds for the delay introduced by the user, which we estimate to be uniformly distributed.
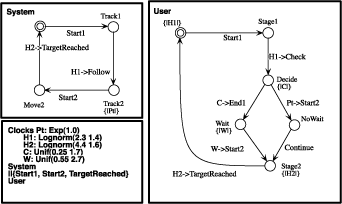
Based on these assumptions, we construct a stochastic process algebra model, presented in Figure 2, that describes the relevant parts of system and user behaviour. We used the model to obtain a histogram of the distribution of the time it would take to reach the target for 10000 different ërunsí of the simulation of the model. Figure 3 presents the simulation results for this model showing the distribution of time until the target is reached for a variety of system performances.
 |
 |
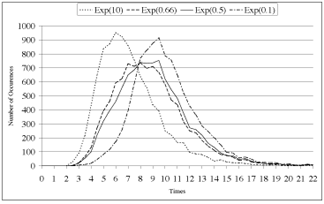 |
| Figure 1: The Magic Board concept. | Figure 2: Finger tracking model. | Figure 3: Results for different tracking performance. |
As we can see, there are two modes, corresponding to the waiting and non-waiting conditions. When system performance is good, the non-waiting mode dominates (curve on the left); as performance degrades, it shifts to a bimodal distribution (curves in the middle), and as it degrades further the waiting mode dominates (curve on the right). The shift to a bimodal distribution corresponds to a system that has an average delay of between ca. 60 and 200 ms. The tracking example above shows how stochastic models could help to visualise the possible impact of assumptions made about user and system behaviour on the overall interaction in the early stages of interface development.
However, the modelling of assumptions about user behaviour requires a very careful approach. There are a number of problems and limitations that have to be taken into account. The best choice of modelling approach may not always be evident, and tool support is still an active area of research.
Conclusions
Stochastic modelling, simulation and analysis using stochastic automata is still a relatively new field. The expressiveness of the specification languages, the theories concerning analysis of specifications, and their incorporation into automated support are still at an early stage of development.
We believe such techniques have an exciting potential for modelling performance in interactive systems, taking into account the abilities and limitations of both user and system. Such models allow us to generate a richer set of answers to design questions, which enables meaningful comparison of the results of an analysis to human factors data and other empirical evidence. Two specific areas for investigation are to look at the different ways in which the approach can be used, and at sources of performance data and how they can be integrated.
Link:
http://kazan.cnuce.cnr.it/TACIT
Please contact:
Giorgio Faconti — CNUCE-CNR
Tel: +39 315 2990
E-mail: Giorgio.Faconti@cnuce.cnr.it