
by Henk Nieland
Tremors caused by an earthquake contain valuable information on its nature. Hence, close examination of these often very fanciful vibration patterns is highly important. CWI has analyzed seismic signals with the wavelet method. It turns out that in this way structures in the signal are revealed that otherwise would remain hidden. The research was carried out jointly with the Dutch National Meteorological Institute KNMI in a project financed by the Dutch Technology Foundation STW.
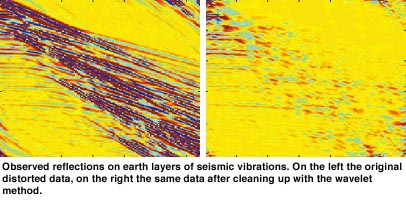
Apart from natural earthquakes, which remain unpredictable so far, there are also those caused by man, in order to explore the structure of the earth’s crust (for example to trace possible oil sources). Vibrations reflected on the higher earth layers are recorded at an observation station and analyzed. Such a seismic signal consists of several waves (phases). Precise determination of the arrival times of two important waves, the P-phase (primary) and the S-phase (shear), is a crucial step in fixing the quake’s type and location. The real art is to extract these two waves from the total signal, in which other waves appear alongside several types of noise. An algorithm based on wavelets was developed that automatically deducts the S-phase from the signal, given the precise arrival time of the P-wave (the S-phase always arrives later). The algorithm was tested at KNMI on more than threehundred ‘local’ quakes (vibrations of gas fields in Groningen, mini-quakes in Limburg and the Ardennes, etc.). The difference with manual determination of the arrival time remained far below the accepted norm and was clearly smaller than what the best method so far could achieve. Before implementation at KNMI for automatic S-wave detection, more tests on a large set of ‘non-local’ quakes (Japan, California, etc.) will follow.

A wavelet is a wave packet of small extension. By shifting it as a mould along the signal, and measuring at every time point how well the fit is, certain features may be revealed which are missed otherwise. The wavelet method, developed since the mid 1980s, is particularly good at detecting sharp transitions or multi-scale (fractal) structures in a signal. It was proposed by the French geophysicist Jean Morlet as an alternative to the traditional Fourier method, which describes a signal (function) as a sum of sine and cosine waves of a certain frequency and amplitude. Because of their infinite extension the fit of such waves with the signal only gives global information (average over the whole signal). In several cases this works well, for example to detect the influence of ocean waves in the wave pattern of the North Sea, but local features are usually missed. Wavelets also have a certain frequency and amplitude, but because of their small extension they are able to describe local features in a signal. Mathematically they are more complicated than the simple sine or cosine functions, but by now the theory is well-established. Wavelets are successfully applied not only in the analysis, but also the processing of signals (efficient storage and transmission of sounds and images). Present research at CWI concerns so-called nonlinear wavelets, with application to information retrieval from multimedia databases.
Please contact:
Patrick Oonincx - CWI
Tel: +31 20 592 4177
E-mail: patricko@cwi.nl