Studying the Heart Left Ventricular Motion with 4D Transformations
by Jérôme Declerck, Jacques Feldmar and Nicholas Ayache
The heart has a vital function in the body. A malfunction may have fatal consequences. Coronary artery disease remains one of the leading causes of death in developed nations. In a large number of instances, the first symptom is a myocardial infarction, and half of the myocardial infarctions cause death. Detecting and preventing this is one of the major goals of modern medicine.
Cardiologists assume that analysis of the motion of the heart, especially the left ventricle (LV), can give precise information about the health of the myocardium. Modern techniques provide 3D images which describe either the anatomy of the heart (eg, MRI) or its functionality (eg, Nuclear Medicine SPECT imaging). It is possible to get sequences of such images over the whole cardiac cycle; such sequences are real 3D movies of the cardiac motion. The cardiac motion, like the motion of any real object must therefore be described as a 4D (3D + time) continuous and regular transformation of time and space.
The purpose of this work is to define a class of 4D planispheric transformations which describes the LV motion, and to develop a method to estimate such a transformation from a sequence of 3D heart images. The transformation is defined in 3D-planispheric coordinates by a small number of parameters involved in a set of simple linear equations. It is continuous and regular in time and space, periodicity in time can be imposed. The local motion can be easily decomposed into a few canonical motions (centripetal contraction, rotation around the long-axis, elevation) that give useful information to the physician for his diagnosis.
For our experiments, we use sequences of gated SPECT (Single Photon Emission Computed Tomography) images, covering the whole cardiac cycle in 8 images. First, points featuring the edges of the left ventricle (endocardium, epicardium) are automatically extracted from the images. We write a 4D least-squares criterion so that its minimisation yields an optimal solution expressed as a 4D planispheric transformation. This criterion involves pairs of matched points over the whole sequence: those pairs are determined and the criterion is minimised using an adaptation of the Iterative Closest Point algorithm.
Once the 4D transformation is obtained, a local analysis is performed: the motion is decomposed into three independent elementary motions featuring:
- a radial motion describing the centripetal contraction that occurs during the systole (first shrinking part of the cardiac cycle)
- a motion along the long axis of the LV describing the shortening and
- a motion describing the rotation around the long axis.
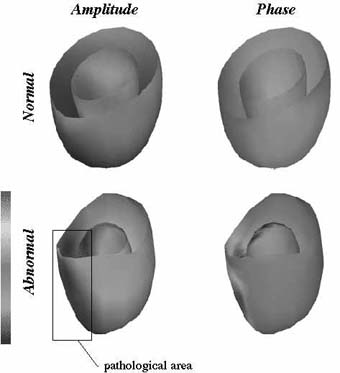
Fourier analysis of the centripetal contraction parameter. On the top,
a normal heart, on the bottom, a pathological case. The surfaces of the
LVs are shaded according to the values of the parameter.
The dependency in time and space allows us to study the evolution of the parameters (centripetal contraction, ...) over time and can potentially reveal pathologies: for instance, the figure illustrates the time analysis performed on the centripetal contraction motion. The amplitude (left) and the phase (right) of the first Fourier harmonic for the parameters values over time are displayed with colors on the surface of the LV. On the top, a normal case; on the bottom, a pathological case suffering from a septal ischemia (reduced blood flow). The ischemia induces an akinesia of the area (the area does not move): the pathological area is located on the left of the images (the septum), the comparison to the normal case reveals its difference (it appears darker because the centripetal contraction is nearly absent) and the type of the pathology (akinesia).
A clinical validation of the protocol is currently under study on a series of gated SPECT images in collaboration with Pr. Michael Goris (Stanford University Hospital) and on tagged Magnetic Resonance images in collaboration with Dr. Elliot McVeigh (Johns Hopkins University). Our hope is that such a software could be used by physicians to better assess myocardial health using non-invasive imaging technology.
Please contact:
Jérôme Declerck - INRIA
Tel: +33 4 93 65 76 63
E-mail: jdecler@sophia.inria.fr
Nicholas Ayache - INRIA
Tel: +33 4 93 65 76 61
E-mail: na@sophia.inria.fr
