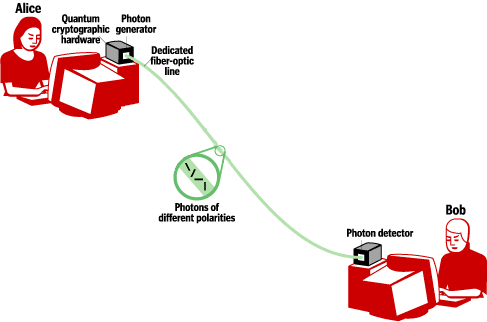
Cryptographic Security by Swamping Adversaries with Quantum Information

by Ronald Cramer and Serge Fehr

In the ongoing quest for cyber security, quantum mechanics plays an increasingly important role. The Cryptology and Information Security Group at CWI in Amsterdam recently designed a new practical scheme for so-called Oblivious Transfer. This is a cryptographic tool known to be sufficient to secure any cooperation among mutually distrusted parties. The new scheme is based on quantum mechanics and the technological difficulty of storing photons without disturbing their quantum state. The basic idea behind the scheme is to swamp an adversary with more quantum information than they can possibly store. According to quantum information theory, the uncertainty a potential adversary has about the total amount of information can be exploited by the honest parties in order to secure private information.

The security of most of the cryptographic schemes in use today is based on the assumption that some computational problem is difficult to solve. For example, the widely used RSA encryption scheme is based on the difficulty of factoring large integers. Part of the research done in the Cryptology and Information Security Group at CWI is devoted to the study of models that allow for cryptographic schemes based on assumptions of a different nature.

One approach is to use quantum-mechanical effects, and to try to base the security solely on the laws of quantum physics, without restricting the adversary’s power. This has proven to be fruitful in the context of Secure Communication, where two mutually trusting communicating parties require security against an outside adversary. However, it falls short of providing security for mutually distrusting communicating parties against each other. This problem is known as Secure Cooperation. A simple but already non-trivial Secure Cooperation is the generation of a random bit, solely by interactive (asynchronous) communication, such that each party is convinced that the bit is not biased against his preference. Another example is the so-called Millionaires’ Problem, where two parties would like to find out who is richer, but in such a way that the wealth of each is not revealed to the other. In general, using Secure Cooperation techniques allows mutually distrusting parties to evaluate any given function on their private inputs – revealing the function value but protecting the individual private inputs.

A fundamental form of Secure Cooperation is Oblivious Transfer. A sender transmits two bits to a receiver, who may choose which one he would like to receive. This is executed in such a way that the sender does not learn the receiver’s choice and the receiver only learns the chosen bit and not the other one. Oblivious Transfer is complete for Secure Cooperation in that, at least in principle, it can be used as a building block to achieve any Secure Cooperation.

Another approach is to design schemes in such a way that a possible adversary is literally swamped with data. He will have to store them all in order to break the scheme, and to obtain classified information and/or provoke a malfunction of the scheme. However honest users of the scheme who are not trying to break it, need only store a small part of the information. Such a scheme is then secure under the assumption that a potential adversary does not have overwhelming memory, even though he might have infinite computing power.

A particularly interesting feature of this so-called Bounded-Storage Model is ‘everlasting security’: if the adversary fails to store the mountain of data during the execution of the scheme, then his chance of breaking it is lost forever together with the data he failed to store. That would never change, even if they should obtain larger storage capacity sometime in the future. This is in sharp contrast to conventional computational cryptography, in which schemes may be broken ‘in retrospect’, once an adversary has gained sufficient computing power. On the other hand, while basing cryptography on computational assumptions allows for very efficient schemes, a major disadvantage of the Bounded-Storage Model is the immense amount of data that must be communicated (even for the honest users) in order to be able to swamp a potential adversary’s memory.

Recently, in collaboration with researchers from Aarhus University (Denmark), CWI’s Cryptology and Information Security Group has put forward and studied a variant of the Bounded-Storage Model which is based on swamping the adversary’s quantum-memory: the Bounded-Quantum-Storage Model. Quantum mechanics provide a good platform for such an approach: on the one hand, according to Heisenberg’s Uncertainty Principle, converting quantum information to classical information by measuring irreversibly destroys some of that information, and the challenge is to arrange it so that the adversary cannot afford this loss while honest users can. On the other hand, in contrast to classical information, storing quantum information is very difficult (at this point essentially impossible), and thus it requires very little to swamp the adversary’s quantum memory.

In this model the CWI researchers have constructed a scheme for Oblivious Transfer, and thus indirectly for any Secure Cooperation. The scheme involves the transmission of a stream of single photons (or other atomic particles), and it is proven secure under the sole assumptions that Heisenberg’s Uncertainty Principle holds and that a potential adversary cannot store more than a large fraction of the transmitted photons, even though he may have infinite computing power and classical memory.

Apart from quantum cryptography, CWI’s Cryptology and Information Security Research Group focuses on all mathematical aspects of cryptology, such as algebraic secret sharing and secure multi-party computation, computational number theory (eg the Number Field Sieve Project for factoring RSA challenge numbers), information-theory-based cryptography, public-key cryptography in general (in particular, chosen cipher-text security for encryption schemes), cryptographic protocols, and formal security analysis.

Link:
http://www.cwi.nl/crypto

Please contact:
Ronald Cramer, CWI, The Netherlands
Tel: +31 20 592 4166
E-mail: Ronald.Cramercwi.nl

Serge Fehr, CWI, The Netherlands
Tel: +31 20 592 4257
E-mail: Serge.Fehrcwi.nl