Large-Scale Simulations of Diffusion in Cell Biology
by Ivo F. Sbalzarini, Anna Mezzacasa, Ari Helenius and Petros Koumoutsakos
Molecular transport within the intracellular structures of live biological cells is dominated by diffusion in confined compartments with complex geometries. Quantitative evaluations of standard experimental assays in cell biology (eg to measure diffusion coefficients of proteins in vivo) require knowledge of the solution of the diffusion equation in such geometries. We present a high-performance parallel implementation of a particle method to solve the diffusion equation in 3D reconstructions of real samples obtained by fluorescence confocal microscopy.
Due to the high structural organization of the intracellular space, diffusion is always restricted to the specific shape of the organelle under consideration. To determine and quantify the diffusive mobility of substances within live cells the technique of fluorescence recovery after photobleaching (FRAP) is widely employed.
From a practical point of view a method is needed to deduce molecular (microscopic) solute diffusion constants from measured fluorescence recovery data. We propose the deterministic particle method of Particle Strength Exchange (PSE) for simulations of diffusion in cellular geometries of realistic complexity. PSE was introduced as an alternative to the method of random walk, enabling higher-order simulations of convection-diffusion processes. PSE is a grid-free, deterministic particle method and thus combines the advantages of high-order convergence and geometric flexibility. It enables efficient simulations of solute diffusion in biological structures using the geometry of real samples.
 |
| Snapshots of the concentration distribution from a sample PSE simulation. The ER membrane is visualized as a transparent surface, and the concentration of the protein under consideration as a volume density cloud inside it. The initial concentration field was 1 everywhere outside the cubic box shown, and 0 inside it. The region of interest around the box is enlarged. |
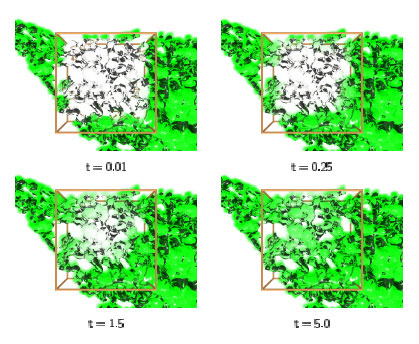
Due to the complex shape of the computational domain, a large number of particles is usually needed to resolve the concentration field. We implemented an efficient parallel PSE code based on a general-purpose Parallel Particle Mesh (PPM) Library currently under development. The code provides different domain decomposition techniques, dynamic load balancing among inhomogeneous processor clusters, parallel file I/O and efficient network communication. It was tested and optimized both on distributed memory and shared memory systems with either scalar or vector processors. Arbitrary geometries can be read in as triangulated surfaces and particles are initialized inside it. (Using a particle method, there is no need for grid generation.)
The method was successfully applied to diffusion in the Endoplasmic Reticulum (ER), which is the most prevalent example of a highly convoluted and interconnected structure in three dimensions. The geometry of several ER samples was reconstructed by recording the shape of the ER samples from live cells using stacks of serial sections obtained by confocal fluorescence light microscopy. It was checked that the reconstructed 3D geometry of the organelle was connected and exhibited all the topological properties of a real ER. It could thus be used directly as a computational domain. Figure 1 shows 3D visualizations of the evolving concentration field inside a sample ER geometry. Using reconstructions from real samples allowed direct comparisons between simulation results and experimental data from the same ER.
Fitting simulated and experimentally measured diffusion curves using time stretching enabled us to determine the unknown molecular diffusion constant in live cells. By using the same geometry both for experiment and simulation, all need for modelling its effect on the apparent diffusion constant is eliminated and the only parameter left is the molecular diffusion constant itself, taking the influences of the specific geometry at hand into full account.
Please contact:
Petros Koumoutsakos,
ETH Zurich/SARIT, Switzerland
E-mail: petros inf.ethz.ch
|
