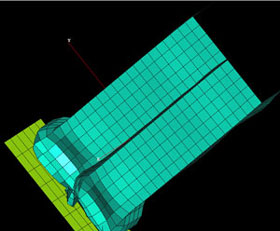
DesParO - A Design Parameter Optimisation Toolbox using an Iterative Kriging Algorithm
by Christof Bäuerle, Clemens-August Thole and Ulrich Trottenberg
DesParO is an optimisation toolbox designed for industrial simulation. The toolbox contains a collection of efficient algorithms for computer-based optimisation and can easily be adapted to any industrial simulation code. DesParO was especially designed for computationally expensive simulation codes and supports parallel computation.
Nowadays simulation programs are widely used in the car industry to optimise production processes or to test the behaviour of a car before a real prototype is built or real tests are performed. Simulation helps to reduce the number of real prototypes and the time between model changes compared to real tests. Crash simulation is one of the most time-consuming simulation tasks and is therefore computationally expensive. Many simulation runs with different parameter values are required to optimise construction parameters, and the results have to be analysed by an engineer. In this case the use of a numerical optimisation toolbox, which analyses different parameter constellations, can support the development process significantly. The optimisation toolbox uses the PAM CRASH simulation program to calculate the crash properties of a car model. For each given set of parameters the simulation results have to be evaluated by an objective function. This article focuses on a box beam test example which demonstrates the applicability of the toolbox to crash simulation problems.
The definition of an objective function which evaluates the crash simulations can be difficult for technical applications. In the case of the box beam example the objective function is constructed as a comparison between a reference crash and a crash of a model with modified material parameters. The aim of this procedure is to define an optimisation problem with a well-known solution to test the toolbox and the optimisation algorithms. In the reference case the acceleration of a box beam with given Youngs modulus and Poisson ratio is calculated and the objective function is defined as the integral of the quadratic differences to the acceleration of a model with modified parameters over the time. This integral can be approximated by a sum over discrete time steps:
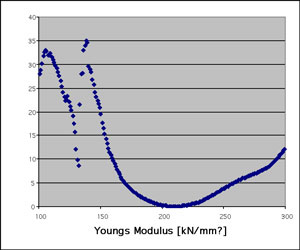
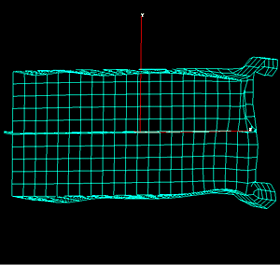
Thus the minimum of this objective function is reached if the material parameters of the modified model reach the values of the reference case.
Figure 2 shows a plot of the objective function versus change of the Youngs modulus. The minimum of this function is at 210 kN/mm2 and is identical with the reference case. Close to its minimum the function is smooth but on the left side the behaviour is rather chaotic. Under realistic conditions, almost all properties of crash experiments are subject to scatter, although it is desirable to avoid the scatter of a model as much as possible. Numerical properties of the simulation codes as well as certain features of the crash model may be responsible for these in-stabilities. Typical sources of scatter which are caused by the model are buckling and contact under an angle of 90°. Further investigation of this effect with the box beam example indicated that the scatter results from an instability between two different modes. Figure 3 shows one such mode. In this case the upper edge on the right side is shifted outward and the lower edge is shifted inward. In the second mode of the model both edges were displaced outside the box beam.
 |
 |
| Figure 1: Crash example box beam. |
Figure 2: Scan of the objective function for the test problem. |
 |
 |
| Figure 3: One possible mode of the crash simulation. |
Figure 4: Convergence of the different optimisation algorithms. |
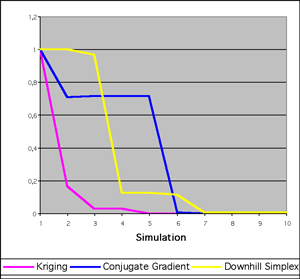
Scatter of a model is a difficult condition for optimisation and an engineer tries to avoid instabilities of a construction. In the test case of the box beam example it turned out to be possible to stabilize the model by a small modification of the construction. In particular, if both edges of the original model are bent to one side it is possible to suppress the asymmetric mode during the crash simulation and the scatter of the objective function can be reduced significantly. This procedure now leads to a well defined optimisation problem.
For the solution of nonlinear problems a wide literature on optimisation strategies is available. Popular strategies are conjugate gradient, downhill simplex, and surrogate models. An important characteristic of the optimisation of crash simulations is that it is usually very time-consuming for a realistic car model. Optimisation strategies based on surrogate models are especially suited for optimisation under such conditions. In the first step design of experiment methods are used to choose parameter values, for which a simulation has to be executed. The values of the objective function for these parameters can now be used to construct a surrogate function as an interpolation of the real problem. The evaluation of the surrogate function is very fast and it is much easier to search for the minimum of this interpolation. During the next steps the design of experiment points can be refined iteratively nearby the minimum of the surrogate function. In Kriging the surrogate model consists of a sum of basis functions, very often of Gauss type. Figure 4 shows the relative convergence of different optimisation algorithms at the stabilized box beam example which was described in this article. Although the Kriging algorithm converges very fast during the first iterations at this problem, the optimisation strategy does not work so reliably if the objective function is not smooth enough.
Future work will concentrate on the aspect of improving the robustness of the surrogate models by replacing the design of experiment methods by pattern search strategies. Furthermore it is planned to extend the surrogate models to unstable crash constructions. In this case surrogate functions are used for approximation (instead of interpolation) of the objective function.
Links:
http://www.scai.fraunhofer.de/35.0.html
http://www.auto-opt.de
Please contact:
Christof Bäuerle Fraunhofer SCAI
Tel: +49 2241 14 27 94
E-mail: baeuerle scai.fhg.de
|
