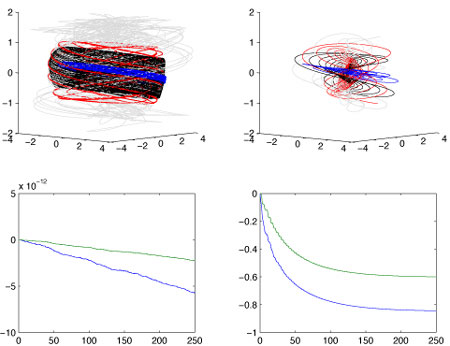
Geometric Numerical Methods for Continuum Dynamics

by Jason Frank

Qualitative properties of numerical simulations of continuum dynamics are studied at CWI using geometric integration. In particular atmospheric fluids were studied with particle-based numerical flow models, in co-operation with Imperial College of London. The ongoing research includes the simulation of ferromagnetic materials.

The project started in 2002, and is funded by the Netherlands Organization for Scientific Research NWO (Innovative Research Grant Veni). The work extends developments in the previous decade in the field of geometric integration, primarily focussed on ordinary differential equations, to continuum systems (fluids, solids) described by partial differential equations.

In many areas of scientific interest, numerical simulations are pushed beyond the limits of classical considerations in numerical analysis such as global error and stability. In molecular dynamics and celestial mechanics, for example, systems that are known to be sensitive to initial conditions are integrated numerically over very long time intervals, despite the fact that the global error has long reached 100 percent. In this case, the user is interested in exploring the qualitative features of the solution rather than in exactly reproducing the trajectory starting from a given initial value.

In the late 1980s and throughout the 1990s, the field of geometric integration arose to develop and analyze numerical methods for ordinary differential equations (ODEs) with the above purpose. Figure 1 illustrates the difference between a geometric integrator and an ordinary method for an ODE of interest in atmospheric dynamics. The most important discovery in geometric integration is that, roughly speaking, a numerical method which retains some property, such as energy conservation or reversibility, actually produces the solution of a perturbed problem with that property. By analyzing the perturbed problem, one can make statements about the quality of the solution far beyond the range of global error analysis. (Hairer, Lubich & Wanner, Geometric Integration, Springer-Verlag, 2002).

Figure 1: Solutions of the 5-component Lorenz model for 4 different initial states, distinguished by colour (top two plots), including one chaotic trajectory (in grey). This model studies geostrophic balance in atmospheric/oceanic fluids. The bottom two plots indicate change in total energy (blue) and enstrophy (green), both of which should be conserved in time. The left two plots are for a geometric integrator, which conserves energy and enstrophy to within 0.01 billionth. The right two plots are for an ordinary method, which damps out more than 80 percent of the energy, and introduces an artificial steady state.

Figure 2: Vortical structures occur on all scales in the atmosphere, hurricanes being a familiar and spectacular example. The study of such structures is very important for our knowledge about the atmosphere. The numerical method of geometric integration, which conserves properties such as circulation, is particularly suited for this purpose (courtesy NOAA/National Climate Data Center, U.S.A.).

Scientists studying continuum processes may also be more interested in the qualitative behaviour of a solution than in the exact solution starting from a particular initial state. One example is climate simulations, which may be carried out over intervals of 100 years or more. Currently, interest in geometric integration is shifting to partial differential equations (PDEs). In some sense, methods for PDEs have had 'geometric' qualities for a long time; the use of monotone methods and Riemann solvers for solving hyperbolic problems is a good example. However, there are new developments as well. CWI, in cooperation with Imperial College of London, has made considerable progress in the last two years in the development of geometric methods for atmospheric fluids using particle-based numerical fluid models. The Hamiltonian Particle-Mesh method combines finite mass fluid particles for advection with a grid for fast evaluation of derivatives, such that the resulting method conserves energy and circulation (vorticity) in addition to mass.

Other research at CWI on geometric integration concerns the simulation of ferromagnetic materials. In particular, the equations governing the flow of magnetic orientation in such materials implicitly define a set of conservation laws for energy and momentum. A numerical method applied to the equations of motion would normally not retain any discrete analogue of such conservation laws. We are currently investigating a method with precisely this property.

Please contact:
Jason Frank, CWI
Tel: +31 20 592 4096
E-mail: jason@cwi.nl
http://www.cwi.nl/~jason/