Dealing with Massives Volumetric Visualisation:
Progressive Algorithms and Data Structures

by Rita Borgo, Valerio Pascucci and Roberto Scopigno

This article summarises recent results obtained in the area of visualization of massive datasets exploiting the strength of subdivision techniques and distribution algorithms. The focus is on trying to meet storage requirements designing visualisation algorithms suitable for distributed environments.

Projects dealing with massive amounts of data need to carefully consider all aspects of data acquisition, storage, retrieval and navigation. The recent growth in size of large simulation datasets still surpasses the combined advances in hardware infrastructure and processing algorithms for scientific visualisation. As a consequence interactive visualisation of results is going to become increasingly difficult, especially as a daily routine from a desktop. The visualisation stage of the modelling-simulation-analysis activity, still the ideal effective way for scientists to gain qualitative understanding of the results of simulations, then becomes a bottleneck in the entire process. This problem poses fundamentally new challenges, both to the development of visualisation algorithms and to the design of visualisation systems.There is a need at system level to design the visualisation process as a pipeline of modules processing the data in stages. In this way a flow of data is created that needs to be optimised globally with respect to magnitude and location of available resources. To address these issues we have been working on a new progressive visualisation algorithm that subdivides the input grid following regular criteria and then traverses the regular structure produced extracting the cells containing isovalues. These cells are then organised in a hierarchical structure (from coarse to fine levels) and subsequent levels of detail are constructed and displayed to improve the output image.

We separate the data extraction from its display. The hierarchy is built by a single process that traverses the input 3D mesh. A second process performs the traversal and display. The schema allows us to render partial results at any given time while the computation of the complete hierarchy is progressing. The regularity of the hierarchy makes it possible to create a good data-partitioning schema that allows us to balance processing time and data migration time. The subdivision criteria is itself suitable for parallelisation. The algorithm works in the following way:

Subdivision: we generate a partition of the input data. Figure 1b shows the 2D edge-bisection refinement sequence that we adopt to sub-sample a 2D regular grid. The coarse level is basically triangular mesh. Each refinement step inserts a new vertex on an edge and splits the adjacent triangles along this edge into two. Instead of 'triangles' we reason in terms of '2D diamonds' considering each cell as the composition of the two triangular halves that will be split by the bisection. For the 2D case we can subdivide the diamonds into two main classes: first class square-shaped diamonds (or type 0 diamonds, Figure 2a), and second class rhombus-shaped diamonds (or type 1 diamonds, Figure 2b). Each diamond is characterised by a centre (the centre of the bisection edge).

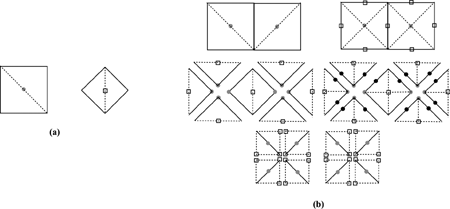Figure 1: a) 2D First and second level diamonds; b) 2D subdivision.

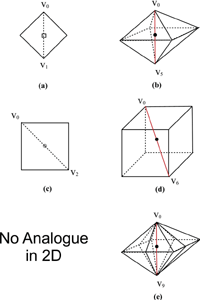Figure 2: 2D diamonds vs. 3D diamonds.

In 3D, the bisection edge refinement becomes a schema for the subdivision of tetrahedral meshes. It applies to tetrahedral meshes in the same way that it applies to 2D triangular meshes. With respect to the 2D case it maintains all the properties. Each cell is still subdivided along 'the longest edge', which corresponds to the main diagonal of the cell itself. Each bisection gives birth to an arbitrary number of diamond-like new cells. For regular grids, the starting cell is a first class cube-shaped diamond cell (see Figure 3a). The bisection of a first class diamond cell gives birth to second class octahedral-shaped diamond cells (Figure 3b-c). Each new second class diamond cell (Figure 3d) is bisected along its main diagonal and third class esahedral-shaped diamond cells are created (see Figure 3e-f). Each esahedral cell (Figure 3g) is bisected along its longest diagonal and generates first class diamond cells (Figure 3h-i). In 3D, we need to repeat the bisection procedure three times to reach a stage in which a new bisection gives birth to first class cube-shaped cells, returning to the subdivision step for the starting cell (see the third level diamond in Figure 2e) .

Hierarchical Organisation: The subdivision schema implies a hierarchical organisation of the dataset. It is easy to organise such a hierarchy in a tree-like data structure and to extract a sort of 'seed set', made up of cells whose internal range of isovalues includes the isovalue target. The seed set generated corresponds to an adaptive traversal of the mesh at different levels. The hierarchy always starts with a first class diamond cell and proceeds through each level of refinement with an alternation of second, third (for the 3D case) and first class diamond cells.

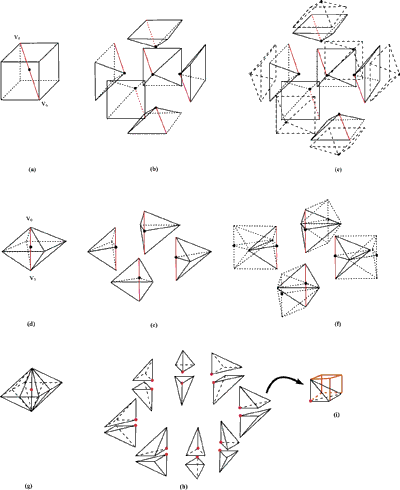Figure 3: First, second and third level diamonds and respective subdivision and fusion with adjacent cells.

Isosurface Extraction: Each generated diamond internally holds a 'piece' of the total isocontour that needs to be extracted. To perform the extraction, for the 3D case, we subdivide each diamond cell into tetrahedra and apply a marching tetrahedra algorithm. Each isocontour is updated within a single tetrahedron and then composed to update the global isosurface within the set T of all tetrahedra around the bisection edge.

The key novelty of the present schema is that, by providing a set of local rules for continuous geometric transitions (geomorphs) of one level of resolution into the next, we bridge the gap between adaptive techniques and multi-resolution decimation-based techniques. Moreover, the regularity of the schema permits the design of an efficient run-time data partitioning and distribution algorithm which will reduce local memory requirements and will make use of the potential of the currently under-exploited distributed environment.

Please contact:
Rita Borgo
Pisa University and ISTI-CNR
Tel: +39 050 315 3471
E-mail: borgo@di.unipi.it

Roberto Scopigno, ISTI-CNR
E-mail: r.scopigno@cnuce.cnr.it

Valerio Pascucci
Lawrence Livermore
National Lab, USA
E-mail: pascucci@llnl.gov