A new Algorithm for Discrete Tomography

by Rob Tijdeman and Herman te Riele

Discrete tomography concerns the problem of recovering binary images from their projections. Recently, Tijdeman (University of Leiden, The Netherlands) and Hajdu (University of Debrecen, Hungary) have made a new mathematical analysis of this problem. In a joint project starting this summer, researchers at Leiden University and CWI will implement an algorithm based on this analysis, such that it can handle large problems, and apply it to the recovery of crystalline structures and the reconstruction of the shape of heart chambers from orthogonal biplane cardiac angiograms.

Discrete tomography has its origin in the analysis of crystalline structures with the help of electron miscroscopy. In particular, one wishes to determine the presence or absence of atoms in a crystal lattice, a two-valued situation (ie, a binary image). Electron rays, transmitted through the material, yield projections of the atom structure of the crystal. The number of projections is limited because the material may get damaged by the transmitted rays.

A binary image is a rectangular array of pixels, each of which is either black (value 0) or white (value 1). A projection of a binary image is defined as a data set which for every line in some direction counts how may white pixels are intersected by that line (the transmitted ray in electron microscopy). This leads to a linear system of equations which, in general, is underdetermined and allows many solutions when only a few projections are available. It turns out, however, that discrete tomography may be quite useful in the case of convex objects such as layers and tumors. In such cases, the solution may well be unique or almost unique. In the case of tumors, the line sums are not exact in general, and so-called noise may affect the correctness of the data set.

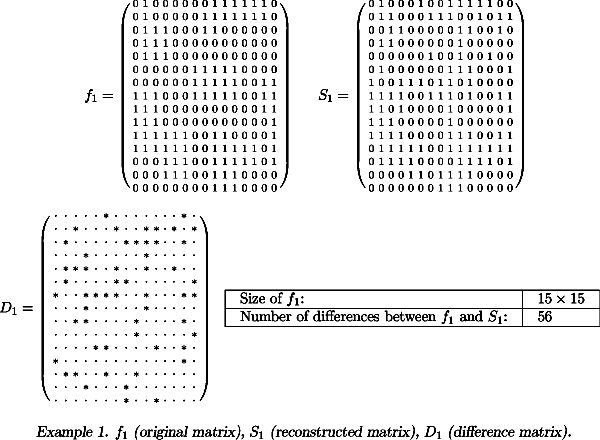Example: f 1 (original matrix), S 1 (reconstructed matrix), D 1 (difference matrix).

The mathematical analysis by Tijdeman and Hajdu of the discrete tomography problem has been published in 2001 in the ‘Journal für die reine und angewandte Mathematik’. Here they study the problem of reconstructing a function which maps a finite lattice of integer pairs in the plane to a subset of the integers. The sums of the function values along a finite set of lines, the projections, are given. It is shown that the possible solution functions form a grid on a linear manifold, and that the solutions with only function values equal to 0 and 1 correspond to points in the grid which have the smallest distance to the origin. It is shown further that there is a basic structure, the so-called switching component, whose translates generate the grid. A simple device is provided to derive the switching element from the set of directions. In a sequel paper, which has appeared in the journal ‘Linear Algebra and its Applications’, Tijdeman and Hajdu apply their theory to the special case of four directions, viz., along rows, columns, diagonals, and anti-diagonals. The resulting algorithm finds a function with exactly the prescribed line sums and with integer pixel values which are small in absolute value. From this, a 0-1 solution with approximately correct line sums is easily obtained. It turns out that for convex patterns of 1’s perfect reconstruction is possible.
In the current project, an implementation of Tijdeman and Hajdu’s algorithm will be improved and extended so that it can be applied to large problems coming from the two application areas mentioned above. The experience at CWI with large-scale computer calculations will be put in here. Since in many practical situations the given line sums are not exact, ie, there is noise on these data, the implementation will be adapted to handle various types of noise. If it is known that the studied objects are more or less convex, not all 0-1 solutions are equally likely to describe the original. It is then convenient to introduce a quality ranking of solutions. A device to select solutions with high ranking will be developed. Finally, the algorithm and its implementation will be extended to cope with ‘grey tints’ so that it will be able to find functions whose range of values is not restricted to 0 and 1, but, eg, to 0,1,2,...,15.

Please contact:
Rob Tijdeman
Leiden University, The Netherlands
Tel: +31 71 5893046
E-mail: tijdeman@math.leidenuniv.nl

Herman te Riele, CWI
Tel: +31 20 5924104
E-mail: Herman.te.Riele@cwi.nl