On Large Random Graphs of the ‘Internet Type

Internet and its infrastructures are growing fast, both in size and in importance. We model the large scale structure of the Internet by a simple model, with a random graph with power-law degree distribution. The nodes represent routers or autonomous systems. We found that in such graphs a spontaneous hierarchy appears with respect to shortest path routing. The length of the paths between typical nodes grows very slowly, as the iterated logarithm (log log) of the number of nodes.

Random networks with power-law distribution of degrees of the nodes have been studied quite extensively in the past few years, at least on a heuristic level (the degree of a node is the number of links connected to that node). By power-law we mean that the probability of having some degree is proportional to that degree raised to some negative constant power, whose absolute value we call the index of the power-law. Such models seem to have some interesting practical applications. In particular, the main characteristics of the Internet graphs follow power-laws on both router and domain levels. These observations may turn out to be significant for topology and routing dependent features of the Internet.

We adopt a random graph model, introduced by Newman, Strogatz and Watts (for all references: see our link at the end). Their original work is, however, restricted to power-laws with indices greater than 3, whereas for the Internet graphs this index lies between 2 and 3, according to the famous empirical study of the Faloutsos brothers by the end of 1990s. Power tailed distributions with index between 2 and 3 have a finite mean but an infinite variance, which entails that nodes with very high degrees appear with a non-negligible frequency. In the regime of Newman et al. it has been shown that the expectation of the distance between two nodes (measured by the number of hops, the usual distance measure on a graph) scales logarithmically with respect to the number of nodes. Such graphs are sometimes called ‘small worlds’. These graphs with index larger than 3 are homogeneous in the sense that in average and asymptotically all nodes have, so to say, the same kind of environment around. This is, however, not the case one would expect for the Internet graph, which has an obvious hierarchy with some powerful nodes having a key role in the functioning of the network. This appears in their large degrees in the graph. On the other hand, a ‘typical’ node does not possess these properties and has a small degree. The method of generating functions used by Newman et al. in their analysis does not work for power-law indices less than 3. In this case they suggested an exponential cutoff in degree distribution and found the same logarithmic scaling for the distance. The exponential cutoff removes the very large nodes and thus changes the character of the graph. We investigated the same model without cutoff and proved that the average distance is at most of the order of the iterated logarithm of the number of nodes.

The model is defined as follows. First we fix the number of nodes. The degrees of the nodes are then genereated as independent and identically distributed random variables following a power-law distribution. The second stage is the random formation of links between nodes. We can think this visually so that ‘link stubs’ sticking out from each node are joined pairwise in a random fashion (if the sum of the degrees is odd, we add one extra node with degree one). As a result, artefacts like multiple links between nodes are possible, but their role is not significant. The third stage is the investigation of properties of such graphs when the number of nodes goes to infinity, a thermodynamical limit. Several phase transitions can be identified when the power law index passes certain critical values. For instance, at value 3 the diameter of the graph changes from logarithmic to iterated logarithm between values 2 and 3, and finally below 2 the diameter is essentially bounded. From the point of view of this physical analogy, the Internet lives in one particular phase.


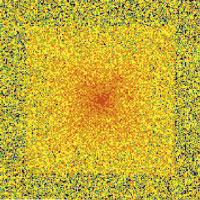
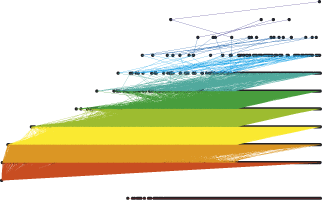
Figure 1: 31624 nodes in quadratic spiral, ordered by descending degree (largest node in the centre, outmost nodes degree 1). The colour code corresponds to closeness to the largest node, and is the same as in Figure 2.	Figure 2: Distance from the largest node. The number of nodes is 31624. The horizontal position of a node indicates its degree while the vertical position shows its distance from the largest one. The links of the nodes are coloured according to their distance from the largest node. The nodes not connected to the largest node are placed on a separate line.


Figure 1: 31624 nodes in quadratic spiral, ordered by descending degree (largest node in the centre, outmost nodes degree 1). The colour code corresponds to closeness to the largest node, and is the same as in Figure 2.	Figure 2: Distance from the largest node. The number of nodes is 31624. The horizontal position of a node indicates its degree while the vertical position shows its distance from the largest one. The links of the nodes are coloured according to their distance from the largest node. The nodes not connected to the largest node are placed on a separate line.

Our task was to find the distance between two randomly chosen nodes in such a random graph with power-law index between 2 and 3. In the limit of large number of nodes, the largest degree in the graph is rather accurately defined. It is proportional to the number of nodes raised to a power that lies between 1/2 and 1. The existence of so huge nodes was indeed apparent from the first study of Internet topology by Faloutsos et al. Such a large node has of course many neighbours. Among them there are almost surely all other large nodes exceeding some minimum degree value. The union of the first neighbours can now be considered as a new, still larger ‘supernode’ having necessarily again a certain number of neighbours, and so on.Within a number of steps that is only an iterated logarithm of the number of nodes, this set is mighty enough to play the role of a ‘core network’. Although the relative size of the core goes to zero as the network grows, the core can be reached from a randomly selected node with less than the same iterated logarithm number of steps. As a result any two such nodes can be connected with no more than of the order of this same number of hops. Formal proofs were done to verify this picture. In the first part, the described reasoning becomes waterproof by elementary arguments when the critical sizes of the ‘layers’ within the core are properly chosen. In the second part, we used a matching with a branching process.

In summary, our work reveals that in a random network where all nodes are in equal position there still exists hierarchy, if the node degrees have infinite variance. According to latest studies, this kind of hierarchy corresponds better to that found in measurements than some traditional deterministic hierarchical network models. The diameter of the graph, in number of hops between nodes, remains almost constant while the graph grows over many orders of magnitude. Both these factors are significant, at least if such a graph can model a communication network, but probably in several other contexts as well.

On Large Random Graphs of the ‘Internet Type’