Angry * (-1) = Surprised!

Facial animation systems allow reproduction of facial expressions on synthetic faces where most of the time expressions are designed by hand. In order to avoid building manually the very large set of expressions humans are able to recognize, why not generate new expressions by combining existing, even very different ones?

The Algebra of Expressions consists of a set of operators and related properties defined over a set that is a generalization of the MPEG-4 Facial Animation Parameters. It may be used to describe, manipulate, and generate in a compact way facial expressions, and adopted as a tool to further study and better understand the role of emotions conveyed by facial expressions and their relationships.

Existing animation tools allow defining facial expressions for human-like or cartoon-like synthetic faces, which are then employed for several purposes in Human-Computer interaction. Most of the tools are designed to build expressions manually, acting on low-level parameters. An example is given by MPEG-4 based tools, where each facial expression is coded as an ordered sequence of 68 integer numbers, called Facial Animation Parameters (FAPs). Parameters 3-68 (that is, 66 of them) act on points defined on a synthetic face (feature points). Each FAP represents a displacement of the associated point with respect to its original position. By displacing a point a deformation of its surrounding area is produced, resembling muscle deformations, and acting on several points facial expressions are created. A neutral expression has all values equal to zero; all other expressions have some FAP different from zero. However, the human face can generate around 50.000 distinct facial expressions, which correspond to about 30 semantic categories. Clearly the human face is extremely expressive. Is it possible to cover this amount by defining a minimal set of expressions as a whole and transforming them, without manipulating directly the set of facial animation parameters? Our suggestion is to define an algebraic structure consisting of three operators and related properties defined over a set that is a generalization of the MPEG-4 FAPs. A Facial State is a set S of 66 integer numbers (s₁, ..., s₆₆) where each element s_i (i = 1, ..., 66) satisfies the constraints defined in the MPEG-4 Facial Animation Parameter definitions table. These constraints require some of the elements to be non-negative. The first operator is called Sum: if we have two facial states S and T, and a weight v, their sum is their weighted mean (see Box 1). The set of facial states is closed under summation. In addition, the Sum operator is neither commutative nor associative in the strict sense, but in a slightly generalized sense both properties remain valid. Also, it does not have an identity. The second operator called Amplifier, is a scalar operator w (a real number) acting on a single facial state S=(s₁, ..., s₆₆): |S·w| = |w·S| = (|w·s₁|, |w·s₂|, ..., |w·s₆₆|). The symbols || denote the approximation to the closest integer. The set of facial states is closed under amplification. The identity value for the amplifier is 1. The third operator is called Overlapper: we can combine two expressions S and T by choosing some regions of the face where only S applies and others where only T applies. The overlapper operator does exactly this, provided that two masks (see Box 2) are defined in order to choose the areas involved in the ‘patchwork’. The set of facial states is also closed under the overlap operation. There is an identity element, but no inverse. The overlapper is both commutative and associative.

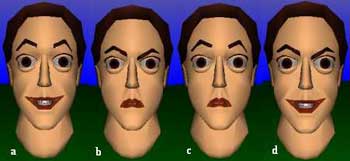Figure 1:
Overlapping expressions. In order we have: smile (a), angry (b),
one overlap (c), and a second different overlap (d).

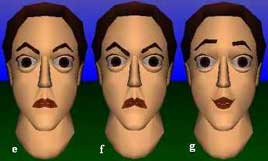Figure 2:
Emphasizing and negating an angry expression.

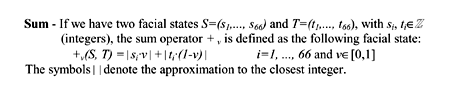Box 1: Definition of Sum.

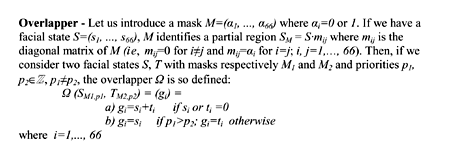Box 2: Definition of an Overlapper.

The operators introduced above have been implemented as methods included in an Application Programming Interface developed in Java. The API has been incorporated as a part of the Tinky system, a facial animation authoring tool developed by the author. Figure 1 shows the use of the overlapper. In (a) a smiling face and in (b) an angry face is shown. The mask associated with (a) covers the mouth area, while the mask associated with (b) covers the eyes and eyebrows areas. Their overlap, according to these masks, is shown in (c), where a surprised expression is resembled. This shows how to derive new expressions from old semantically different ones. By using the same expression switching the role of the masks a different overlap is produced, as shown in (d): the mouth is smiling and the eyes are angry. Again, this expression is semantically different from the previous ones, signalling smartness, arrogance or sense of superiority. In Figure 2 an angry face (e) is emphasized using the amplifier w = 2 (f) and has been inhibited by w = -1 (g). Indeed, we have found that negative values produce accordingly a negation of the expression. The negation of a smiling face seems to be a sad face, the negation of an angry face results in a surprised face, although further research needs to be done in this area to justify more general statements. Possibilities to combine expressions are countless. For example, any expression can be made asymmetric, by joining its left part with its enhanced right part (ie using the overlapper and the amplifier). Currently we are engaged in the development of ad-hoc formulas with which we may define and represent transformations of facial expressions, like asymmetric expressions, negations of expressions, derivative expressions, combinations of emotions and visemes, etc. We are also engaged in developing an animation algorithm able to exploit this algebra and use its constructs as key-frames of animations. In such a sense an effort of defining an algebra of animations, which has the task of formalizing the structure of such an algorithm, is currently under development as well.