Iterative Methods in Image Reconstruction

A research group of scientists from the Departments of Informatics and Mathematics of Pisa University and from the Institute IIT-CNR, is working in image reconstruction problems in the areas of medicine and astronomy. It was found that practical iterative solutions are possible by using suitable preconditioners which increase the rate of convergence without mixing the signal (ie the original image) and the noise (ie small errors on the data).

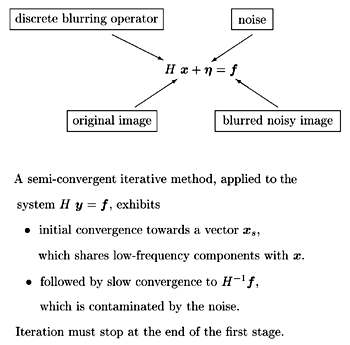
Image reconstruction is an inverse problem consisting of the identification of the input of a given instrument from the knowledge of its output. Inverse problems are generally ill-posed: they might not have a solution in the strict sense, solutions might not be unique and/or might not depend continuously on the data. The discrete version of the image reconstruction problem is a linear algebraic system, that is well-posed in the sense that it has a unique solution. However, this solution is completely corrupted by the noise, and is physically unacceptable because it generally does not reproduce the data within the experimental errors. This difficulty can be overcome by ‘regularization’, ie, by incorporating some expected physical properties of the object in terms, for example, of constraints on the size or on the smoothness of the solution. Starting from this idea, Tikhonov regularization methods solve least-squared problems depending on a regularizing parameter.

As an alternative some iterative methods, which enjoy an interesting regularization property known as semi-convergence, can be used. A semi-convergent method starts reconstructing the low-frequency components of the solution; then, as the iteration progresses, the high-frequency components are reconstructed together with the noise components. Hence the method must be stopped before it starts to reconstruct the noise. The classical conjugate gradient (CG) method, which applies to symmetric positive definite systems, has the regularizing property.

Due to ill-conditioning of the problem, the number of iterations required by CG to obtain a satisfactory result can be large and a preconditioning technique is required to increase the rate of convergence. This rate depends on the number of distinct eigenvalues of the matrix associated with the problem, and general purpose preconditioners are designed to cluster all eigenvalues around 1.

In the present context, this type of preconditioner would be harmful, mixing the signal and the noise, whereas only the eigenvalues corresponding to the low-frequency components of the signal should be clustered. In many applications, the function which describes how the imaging system affects the points of the original image (the so-called point spread function) is space invariant with respect to translations (in this case it is determined by the image of a single point source) and is band-limited (ie it has a local action, a single source of light is blurred into a small spot, wherever the source is located).

Figure 1:
Discrete image reconstruction problem.

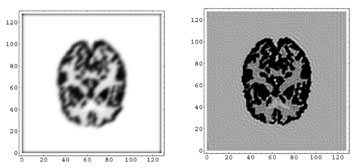Figure 2:
Left: Blurred image of a Hoffman phantom.
Right: Reconstructed image after 5 iterations of a preconditioned conjugate gradient method.

These properties result in a strong structure of the matrix of the linear system, which turns out to be a two-level band Toeplitz matrix. A band matrix has non- zero elements only on a few diagonals around the principal one, and a Toeplitz matrix has equal elements on each diagonal. A two-level band Toeplitz matrix is a block matrix which presents these two structures (band and Toeplitz form) both at the block level and inside each block. Circulant preconditioners, frequently applied to Toeplitz matrices, can be easily modified in order to cope with the noise. However, in the case of band Toeplitz matrices, a band preconditioner would be preferable, since it could be inverted with the same cost of a CG iteration. We have recently proposed a two-level band preconditioner, which is effective for image reconstruction problems with the above properties and has a computational cost per iteration linear with respect to the number of pixels of the image. Figure 2 shows an example of a synthetic medical image (the 2D Hoffman phantom) blurred by the instrument used for acquisition and corrupted by noise. Figure 3 shows the image reconstructed by applying a few iterations of a preconditioned CG method.

Please contact:
Paola Favati, IIT-CNR
Tel: +39 050 315 2412
E-mail: favati@iit.cnr.it