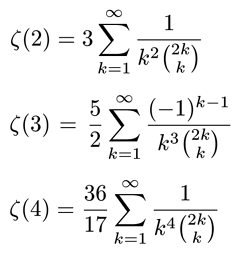Experimental Mathematics and Integer Relations

The emergence of powerful mathematical computing environments, growing availability of correspondingly powerful (multi-processor) computers and the pervasive presence of the Internet allow mathematicians to proceed heuristically and ‘quasi-inductively’. Its exciting consequences have been studied over the past ten years at the Centre for Experimental and Constructive Mathematics of Simon Fraser University, Canada. They include several recent results connected with the Riemann Zeta Function.

Mathematicians increasingly use symbolic and numeric computation, visualisation tools, simulation and data mining. This is both problematic and challenging. For example, we mathematicians care more about the reliability of our literature than other sciences. These new developments, however, have led to the role of proof in mathematics now being under siege.
Ten years ago I founded the Centre for Experimental and Constructive Mathe-matics (CECM) and wrote: “At CECM we are interested in developing methods for exploiting mathematical computation as a tool in the development of mathematical intuition, in hypotheses building, in the generation of symbolically assisted proofs, and in the construction of a flexible computer environment in which researchers and research students can undertake such research. That is, in doing Experimental Mathematics.” At present, the ‘mathematical universe is unfolding’ much as anticipated.

Many of my favourite examples originate in between mathematical physics and number theory/analysis/knot theory and involve the ubiquitous Zeta Function, of Riemann hypothesis fame. They rely on the use of Integer Relations Algorithms: A vector (x₁, x₂,..., x_n) of real numbers possesses an integer relation if there are integers ai not all zero with

The goal is to find ai if such exist, and if not found, to obtain lower bounds on the size of possible a_i.

For n = 2, Euclid’s algorithm gives the solution. The first general algorithm was found in 1977 by Ferguson and Forcade, followed by Lenstra, Lenstra and Lovász (LLL) in 1982, implemented in Maple and Mathematica, and my favourite PSLQ (Partial Sums using matrix LQ decomposition) in 1991, with a parallel version in 1999. Recently, J. Dongarra and F. Sullivan ranked Integer Relation Detection among ‘the 10 algorithms with the greatest influence on the development and practice of science and engineering in the 20th century’. (Some others: Monte Carlo, Simplex, FFT.)

A CECM interface allows one to find relations and explore the underlying algorithms. Three examples are presented in the Boxes: 1. Algebraicness, 2. Riemann Zeta Function, 3. Binomial Sums.

1. Algebraicness

An immediate very useful application is to determine if a number is algebraic. We compute a to sufficiently high precision (up to n₂ digits) and apply LLL to the vector (1, a, a₂, ..., a_n-1). Solution integers a_i are coefficients of a polynomial likely satisfied by a. If no relation is found, firm exclusion bounds are obtained.

3. Binomial Sums

formula 1

2. Riemann Zeta Function

The Riemann Zeta Function is defined, for s > 1 by

Thanks to Apéry (1976) it is known that

formula 2

These suggest that

is a simple rational or algebraic number.

Sadly, or happily, PSLQ tells us that if Z₅ satisfies a polynomial of degree &Mac178; 25 the Euclidean norm of coefficients exceeds 2 x 10³⁷. And the order and norm can be extended at will.

Results in Box 3 were obtained via Gosper’s (Wilf-Zeilberger type) ‘telescoping algorithm’ (see also Paule’s contribution in this issue). Identity (3) was recently proved by Almkvist and Granville (Experimental Math, 1999) thus finishing the proof of (2) and perhaps shedding light on the irrationality of

(7)? —

(2N+1) is not proven irrational for N > 1, though it is now known that one of

(3,5,7,9,11) is!

Many other similar triumphs, and an equal number of failures are described in the references given below, in fields as diverse as quantum field theory, nuclear magnetic resonancing, probability, complexity, algorithm design, and coding theory:

Please contact:
Jonathan M. Borwein,
Simon Fraser University, Canada
Tel: +604 291 3070/5617
E-mail: jborwein@cecm.sfu.ca