Computational Topology Techniques for Shape Modelling

by Silvia Biasotti, Bianca Falcidieno, Michela Mortara, Giuseppe Patané and Michela Spagnuolo

Shape understanding, as a fundamental skill for object description and representation, can traverse several application fields. In this context, mathematics provides shape descriptors, which can be successfully applied to shape analysis.

Research activity at the Istituto per la Matematica Applicata e Tecnologie Informatiche (IMATI-CNR) relates to the mathematical background and application understanding that lies behind the representation and generation of shapes in computer graphics and vision. In particular, we focus on issues related to the definition of abstraction tools for high-level descriptions of complex shape models.

For many years researchers at IMATI-CNR have been working on different aspects of shape-based modelling. Characterising a shape means construc-ting a computational description of the most representative features of the shape, usually a few basic types, along with their relationships (structural decomposition). This approach generally produces a graph-based representation of a shape which is decomposed into basic shape elements, or features, which should have certain properties: elements should not change under translation, rotation or scaling (invariance); the description should be locally insensitive to modification of the shape occurring far from the current focus (rich local support), and a small perturbation of the shape should produce only a small perturbation of the description (tolerance to noise). Unfortunately, it is rather difficult to define shape descriptors which fulfil all these requirements, but interesting possibilities can be explored to find a reasonable trade-off among the various possibilities. Recently, computational topology has been proposed as a branch of computational mathematics with the aim of solving problems related to topological issues, without neglecting the feasibility or the computational complexity of the problem.

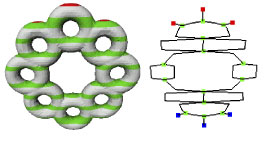
Shape interpretation is especially relevant for the perception of complex forms, in which the ability to vary the level of descriptive abstraction is the key to recognizing and classifying highly complex shapes. From a mathematical point of view, classical tools, such as Morse theory, homotopy and homology, would appear to be appropriate for dealing with topological questions in computer applications. In fact, homotopy and homology are branches of algebraic topology which deal with topological invariants such as the number of connected components, holes, etc. of a given manifold (in our case a surface). Our approach to shape description is based on the classical Morse theory and would seem to be suitable for analysing any data that can be modelled as a surface. More precisely, given an object surface S and a smooth real valued function f defined on it, Morse theory provides the relationship between the critical points of f (which informally can be thought as points where the tangent plane is horizontal) and the global topology of the surface S. In this context, Morse functions, ie the set of real functions whose critical points are non-degenerate (that is, the gradient of f calculated in those points is zero and the ‘Hessian’ matrix of second derivatives is non-singular), have been extensively studied. Under such hypotheses on f, Morse theory states that the shape of the pair (S, f) is represented by the sequence of the homology groups of the level sets, that is the set of points P on S such that f (P) is smaller than a given real number x. Moreover, the critical points of f determine the homology groups of S. Since the homology and homotopy groups codify shape properties as the number of connected components, holes and cavities of an object, it follows that a finite collection of level sets is sufficient to fully describe the surface shape, and is more complete than simply knowing the global homology. Focusing on the topological changes of level sets by varying x, we obtain a discrete description which effectively represents the shape of S and can be encoded into a topological graph, called a Reeb graph. This graph is a subset of S where points having the same value through f are identified if their pre-images are in the same connected component. Therefore, the topological changes of the surface contour levels are coded making it possible to define how the cells corresponding to several critical points glue together (see Figure 1).


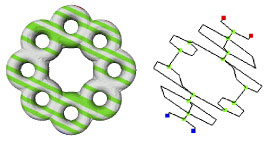
Figure 1: A topologically complex object and its Reeb graph.	Figure 2: The Reeb graph of the object in Figure 1 extracted with respect to a different direction.
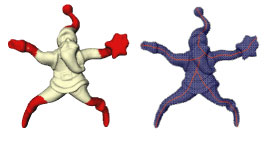	Figure 3: A skeleton of an object extracted as a Reeb graph using a non-Morse function.

Although the global homology of the surface S does not change by varying the function f, the topology of level sets depends on f. In this way the choice of the representing function f determines a collection of shape descriptors whose properties depend on the function itself, thus characterizing the object surface by taking into account the application context. Possible choices of f are the directions in the three-dimensional space (see Figure 2).

Furthermore, in cooperation with other research groups in computational mathematics, we are also trying to extend the theory to non-Morse functions and we are investigating the application of affine-independent functions. In particular, our research efforts are moving onto functions which do not depend on the orientation. For example, we have proposed a mixed strategy for extracting the skeleton of a surface represented through a simplicial complex, which combines homology with differential and computational topology techniques, (see Figure 3).

Please Contact:
Silvia Biasotti, Bianca Falcidieno,
Michela Spagnuolo, IMATI-CNR
Tel: +39 0106 4751
E-mail: {silvia,bianca,michi}@ima.ge.cnr.it