|
ERCIM News No.50, July 2002
|
Simulation of Underground Water Pollution
by Mario Arioli
The Numerical Analysis Group at Rutherford Appleton Laboratory develops new algorithms and mathematical software that are used in several key sectors of applications. In collaboration with other teams of ERCIM (the Italian IAN-CNR and the Computer Science Department of the Czech Academy of Science), the group has started a new research project related to the study of the mathematical and numerical aspects of the underground water pollution problem.
The main objective of this research is to provide efficient and reliable numerical algorithms for the simulation of the underground flux of a liquid. Underground 3-D flow modelling plays a key role in several physical phenomena and engineering processes such as oil reservoir exploitation and underground water remediation. In particular, it plays a relevant role in the simulation of the decontamination process of the area around the Stráz pod Ralskem uranium mine in the Czech Republic, and we compare several of our algorithms on a set of 3-D test problems coming from this problem (Arioli, Maryvska, Rozlovzník, and Tuma, 2001, RAL-TR-2001-023).
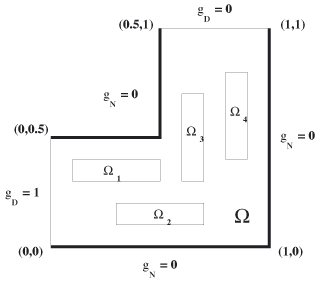
Darcy’s law describes the relationship between the pressure p(x) (the total head) and the velocity field u(x) (the visible effect) in ground-water flow. In Figure 1, we see how Darcy’s law relates the vector field u to the scalar field p via the permeability tensor K(x) which accounts for the soil characteristics, and the divergence of u to the source-sink term f(x). In Figure 2, we give an example of the domain.
In order to solve Darcy’s law, we use mixed finite-element approximation techniques. This leads to the solution of an augmented, nonsingular, and sparse system of linear equations (see Figure 3). For real 3-D problems the system can have several million unknowns. To solve this system, we apply a specialized version of the classical null space algorithm for the minimisation of linearly constrained quadratic forms. This approach has the advantage of preserving the physical meaning of the computed velocity field u because it imposes the conservation of the flux. In the null space algorithm, first we compute a basis of the null space defined by the flow conservation equation, then we solve a reduced linear system on the null space by the conjugate gradient algorithm, implicitly computing the matrix-vector products.
Indeed, MA49 from the HSL 2002 library (see http://www.cse.clrc.ac.uk/Activity/HSL) gives the possibility of using its sparse result for implicitly computing all the matrix-vector products required by the algorithm. Moreover, the number of steps performed by the conjugate gradient method is independent of the mesh size (Arioli and Manzini, 2002, Comm. Num. Meth. Eng.). However, we point out that, for 3-D problems, storage can be prohibitive (see Figure 4). For this reason, we use a novel approach based on network programming techniques. Using the Shortest Path Tree algorithms, we identify a basis of the null space by simple permutation matrices (see Figure 4). Because we require a negligible amount of additional storage, our code is competitive for large problems where the storage required by general purpose direct solvers can be prohibitive. In particular, when the test problem has a unit square domain and K(x) has a random distribution with its values ranging from 1 to 10-12, our approach is competitive in terms of CPU time with MA47 of the HSL 2002 library (Arioli and Manzini, 2001, RAL-TR-2001-037).
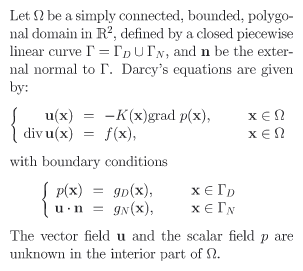 |
 |
|
Figure 1: Darcy’s law. |
Figure 2. |
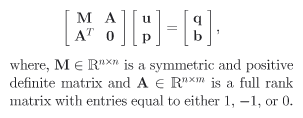 |
 |
| Figure 3: Augmented System. | Figure 4: Null Space Algorithm (click on the image for figure in full size). |
Please contact:
Mario Arioli, CLRC
Tel: +44 1235 445332
E-mail: m.arioli@rl.ac.uk
