Modelling SAR Images of Urban Areas

Satellite imagery has found vast applications in a wide spectrum of areas including agriculture (eg detection of crop types), urbanization (tracking the development of urban areas), cartography (eg detection of rivers, road networks), warfare (eg detection of targets, surveying), etc. This heavy demand on satellite imagery applications lead to the development of imaging systems that are alternative to optical imagery. In particular, synthetic aperture radar (SAR) imagery in the last two decades has become increasingly popular as some of its properties are favorable to optical imagery. SAR imagery can operate regardless of weather conditions and SAR image resolution is independent of sensor height.

There are problems associated with the nature of radar imaging process. SAR images are formed by the reflections of waves from the earth surface. If the surface roughness is comparable to the wavelength, the wave reflections occur in various directions. These directions are also dictated by the incidence angle, surface structure, dielectric constant of the surface, too many factors to be successfully accounted for by a simple deterministic model. The coherent addition of these reflected waves in the receiver out-of-phase results in the granular appearance of the images which is referred to as speckle noise.

The assumptions of the classical SAR image generation model lead to the convention that the real and imaginary parts of the received wave follow a Gaussian law, which in turn means that the amplitude of the wave has a Rayleigh distribution. This classical model has been successful in some cases such as modelling particular natural scenes. However it is known that it fails to provide an efficient model for urban scenes where man-made structures provide bright reflections. The impulsiveness of these images suggests underlying heavy-tailed clearly non-Rayleigh distributions. Some alternative distributions have been suggested such as the Weibull and log-normal distributions, however, in most cases these models are empirical, and do not generalise. By relaxing some of the assumptions leading to the classical Rayleigh model, we have developed a more general and successful model for SAR images of urban areas.

The classical SAR image formation model assumes that the reflections that add up in the receiver are Gaussian due to the central limit theorem. However, this model does not consider the attenuation that is faced during the wave propagation. Consideration of this attenuation leads to a more general model for the received signal which is alpha-stable distributed. This is in accordance with a generalised version of the central limit theorem. Recent work on multiuser communication which has a similar model for wave propagation and the distribution of sources also led to the alpha-stable model. Alpha-stable distributions have received wide interest recently as efficient models for impulsive data and have found applications in radar signal processing, financial time-series analysis, communications and audio signal processing. They are generalisations of the Gaussian distribution and are governed by two additional parameters one setting the impulsiveness, the other the skewness (unsymmetry) of the distribution.

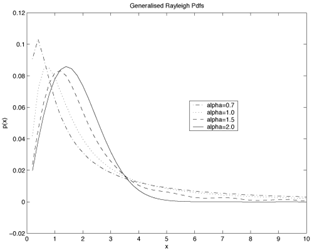
It can be shown that starting from alpha-stable assumption for the complex parts of the received wave, the amplitude is distributed with a generalisation of the Rayleigh distribution which we call heavy-tailed Rayleigh distribution. This distribution has two parameters setting the dispersion and the impulsiveness of the distribution. A group of these distributions is plotted in Figure 1 for varying values of the impulsiveness parameter.

For this model to be of any practical use, efficient algorithms for estimating the model parameters are needed. We have thus also derived novel methods for the estimation of the heavy-tailed Rayleigh distribution parameters based on negative fractional-order statistics which are of great interest in themselves since this is one of the first applications of the new concept of negative fractional order moments. Our experimental results show that the heavy-tailed Rayleigh model can describe a wide range of data which could not be described by the classical Rayleigh model.


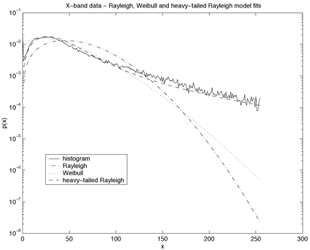Figure 1: Generalised Rayleigh probability density functions for various values of impulsiveness parameter.	Figure 2: X-band SAR image.	Figure 3: Histogram of the X-band SAR image, and fittings of classical, generalised Rayleigh and Weibull models in logarithmic scales.

In Figures 2 and 3, we provide the results of some simulations on SAR images of urban areas. It is clear that the new generalised (heavy-tailed) Rayleigh distribution provides a better statistical description for the SAR images of urban areas when compared to the classical Rayleigh model and other alternative models suggested in the literature such as the Weibull distribution. The estimation technique we suggested also makes it more attractive than other heavy-tailed models such as the K-distribution for which model parameter estimation is particularly difficult. A wide survey on images taken at different bands and weather conditions (such as humidity) would provide us with a relationship between model parameters and imaging conditions which would be very useful in interpreting SAR images.

Please contact:
Ercan E. Kuruoglu — IEI-CNR
Tel: +39 050 315 3128
E-mail: kuruoglu@iei.pi.cnr.it