ERCIM News No.44 - January 2001 [contents]

Reverse Engineering Shapes

by Tamás Várady

In many areas of engineering, medical sciences or art there is a strong demand to create an appropriate computer representation of existing objects from huge sets of measured data points. This process is called reverse engineering of shapes. While this topic has been an important topic in computer vision, due to the advances in laser scanning, now it has become a realistic expectation in the geometric modelling community to generate accurate and topologically consistent models, ready to be used in CAD/CAM. Recent research results of the Geometric Modelling Laboratory at SZTAKI are reviewed within the framework of the whole reverse engineering process.

In conventional computer aided design the computer representation of objects are created by means of commands typically using an interactive design program with 3D graphics. This representation is used for further design, analysis and optionally for numerically controlled manufacturing. While conventional engineering transforms engineering concepts and models into real parts, in reverse engineering real parts are transformed into such computer models which are suitable to exploit all advantages of modern CAD/CAM technologies and transfer real objects into virtual reality environments.

Typical applications include reproducing and redesigning parts, when no original drawings or documentation are available. In areas where aesthetic design is particularly important - such as in the automobile industry - real-scale wood or clay models are often needed, because stylists prefer to evaluate real 3D objects rather than 2D screen images at reduced scale. Another important area of application is to generate custom fits to human surfaces, for mating parts such as helmets, or prostheses.

The Geometric Modelling Laboratory at SZTAKI, Budapest has been conducting reverse engineering research since 1995. This activity has been supported by various grants including an EU COPERNICUS grant (RECCAD) and several smaller ones by the Hungarian Scientific Research Fund (OTKA). Research has been focused to develop fundamental techniques to process and create accurate geometric models and also to exploit the theoretical results in various applications. (See the web pages of GML and its spin-off company Cadmus Ltd. at http://www.cadmus.hu.) The process of reverse engineering is decomposed into the following steps: data capture, preprocessing measured data, merging multiple point clouds, creating the topology of the object by forming a triangular mesh, simplifying meshes, segmenting point clouds, fitting surfaces, building boundary representation models, adding blending surfaces and finally ëbeautifyingí models. Maybe the most crucial part is the segmentation of the point cloud: subsets of points need to be separated from each other according to their fundamental geometric or functional properties. Once we have this information, we can fit surfaces to the individual point sets, but without this or with incorrect segmentation the final result is likely to be wrong. For example, if we have a subset of points with rotational symmetry, but we fail to separate all corresponding data points and include wrong points, the ëbest fití rotational surface may be distorted. If we detect only a shrunk subset of the rotational portion, our estimate will not be too accurate.

This problem is even more difficult for free-form surfaces, where there are unknown smooth edges between the individual surface elements, which need to be separated. A new paradigm called ëfunctional decompositioní helps in these situations. A free-form object is assumed to be bounded by relatively large primary surfaces plus connecting surface elements called feature surfaces, such as blends or steps. In the reconstruction procedure first we create primary surfaces over topologically irregular regions with several holes, and enforce smoothness to assure fair shapes and natural extensions outside the given point regions. Then we fit feature surfaces, which are constrained to be smoothly connected to the primary surfaces. In this way, based on partial point information, we can get complete CAD models having the likely original surface components by means of which the object might have been originally constructed (see Figure 1).

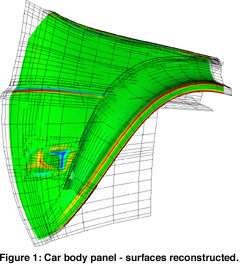
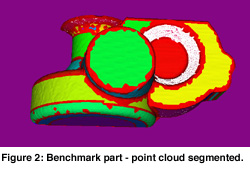
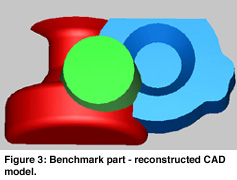
For conventional mechanical engineering objects a different approach - ëdirect segmentationí has been developed. In this context, conventional means bounded by simple analytic surfaces, swept surfaces and blends. These objects have many faces, which typically intersect each other, but the surface elements are much simpler from geometric point of view. Linear extrusions and surfaces of revolutions are particularly important here, and need to be detected and accurately reconstructed based on their ëregularity ë. Having this limited, but very important class of surface elements, it is possible to perform segmentation without user interaction. This is illustrated in Figure 2, where different colors has been assigned to segmented point sets. In Figure 3, the corresponding reconstructed CAD model is shown. Note, that smoothness between neighboring surface elements is assured, once their likely smoothness has been detected. For example, rotational symmetry was detected for the left part of the object, consequently the reconstructed torus and cylinder pieces will be joined smoothly in strict mathematical sense. Engineering constraints, such as parallelism, perpendicularity, concentricity and others can also be recognized thus the final model will satisfy these as well.

The diversity of reverse engineering problems has provided and still provides many interesting research topics for the Geometric Modelling Laboratory. By now this technology has reached an advanced level, and it is being directly exploited in various CAD environments. Our current partners are from the automotive and medical industries.

Links:
Geometric Modelling Laboratory at SZTAKI: http://www.sztaki.hu/gml/

Please contact:
Tamás Várady - SZTAKI
Tel: + 36 1 386 8782
E-mail: varady@sztaki.hu