
ERCIM News No.44 - January 2001 [contents]

![]()
ERCIM News No.44 - January 2001 [contents]
by Anatoly Fomenko, Stanislav Klimenko and Igor Nikitin
The Virtual Environments Group at the GMD Institute for Media Communication has developed methods of computer visualization to understand complex dynamical systems in physical research, like string theory or time-symmetric electrodynamics.
Investigation of dynamical systems in theoretical physics is often reduced to analysis of properties of certain geometrical objects, particularly, surfaces, characterizing the physical state of the system. Singularities of such surfaces correspond to critical phenomena in underlying dynamics. Methods of computer visualization can help to understand a structure of singularities on characteristic surfaces, shed light on deep mechanisms of complex physical processes and give inspiration necessary to find a solution of the problem.
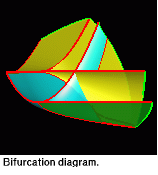
Topological Atlas of Integrable Cases in Rigid Body Dynamics
In Hamiltonian mechanics of a rigid body there is a wide class of special (integrable) cases, for which the motion of a body has stable, regular properties. The most well-known of them are the so-called Euler, Lagrange and Kovalevskaya cases. In spite of the fact that during the last 100 years a large number of papers and even monographs have been devoted to the investigation of their properties, since only recently the analysis of their global topology is performed. It turns out that computer and visualization methods work very effectively in this field, and sometimes allow to solve new purely analytical problems. The project combines the two approaches: classical analytical methods and computer visualization to investigate such integrable cases. Particular result, obtained in the project, is visualization of bifurcation diagram for Kovalevskaya top, a surface, subdividing the phase space of the system to regions, where the top has topologically different types of motion.
String Theory
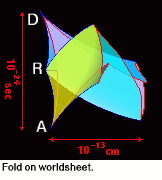
String theory is a contemporary model of elementary particles, which presents them as a system of point quarks, connected by a string-like tube of chromodynamical field. The evolution of strings is governed by the following dynamical principle: surfaces, swept in motion of the string through the space-time, called worldsheets of strings, are extremals of area functional in Minkowski space-time. In other words, worldsheets are non-Euclidean analogs of soap films.
One of the interesting properties of such surfaces is existence of topologically stable singularities, correspondent to points of energy concentration inside elementary particles. Recent research, based on visualization of worldsheets, detects solutions of new type, whose density of energy changes sign in passage through the singularities. Correspondent worldsheets have folds, like shown in the figure. Slices of the fold by planes of constant time produce the following string evolution: appearance of string component with total zero energy from vacuum in point A, its recombination with main positive energy string component in point R and disappearance of resulting zero-energy string component in vacuum in point D. In this way the usage of visualization methods allows to demonstrate instability of vacuum state in string microworld.
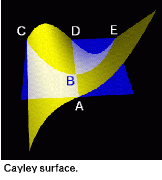
Time-symmetric Electrodynamics
Theoretical physics knows several examples of dynamical systems, which incorporate direct influence of future to the present, ie the systems with equations of motion x''(t) =F(x(t+1)) or similar. One such system, called time-symmetric electrodynamics, was introduced in the beginning of 20th century, and strictly formulated in works of Wheeler and Feynman in 1949, who had shown full mathematical consistency of such theory. Since this time the model of Wheeler and Feynman attracts the interest of theoretists. Particularly, structure of solutions in a problem of 1-dimensional relativistic scattering of 2 particles in time-symmetric electrodynamics is defined by properties of stationary manifold of Poincare map. Visualization of this manifold shows, that it has a shape of Cayley surface, one of elementary surfaces in the catastrophe theory. As a result, at a certain critical value of velocity of colliding particles, equal to 93.7% of light velocity, solution undergoes elementary catastrophe of bifurcation (splitting): in point B one solution (A) splits into three (C,D,E). Pictures of scattering for solutions A,D have a symmetry under spatial and temporal reflections, while such pictures for solutions C,E are not symmetric, but transformed one to another by reflections. Thus, the bifurcation is followed by an effect of spontaneous breaking of mirror symmetries in studying dynamics.
Links:
Homepage of the project: http://viswiz.gmd.de/~nikitin/viz.html
Please contact:
Igor Nikitin - GMD
Tel: +49 2241 14 2137
E-mail: Igor.Nikitin@gmd.de