ERCIM News No.44 - January 2001 [contents]

Static Solution for Real Time Deformable Objects with Fluid Inside

by Ivan F. Costa and Remis Balaniuk

The Long Elements Method (LEM) is a new method for physically based simulation of deformable objects, suitable for real time animation and virtual environment interaction. The approach implements a static solution for elastic global deformations of objects filled with fluid based on the Pascal’s principle and volume conservation.

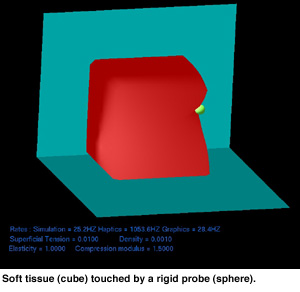
Physically based simulation of deformable objects is a key challenge in Virtual Reality (VR). LEM was conceived for soft tissue real time simulation, particularly for surgical simulation. The priorities in this kind of application are: unrestricted multi-modal interactiveness, including interactive topological changes (cutting, suturing, removing material, etc), physically based behavior, volumetric modelling (homogeneous and non-homogeneous materials) and scalability (high accuracy when needed). The choices made to define the method were driven by these priorities.

The approach is based on a static solution for non-linear elastic deformations of objects filled with uncompressible fluid, what is a good approximation for biological tissues. The volumes are discretised in a set of Long Elements (LE), and an equilibrium equation is defined for each element using bulk variables. The set of static equations plus the Pascal principle and the volume conservation are used to define a system that is solved to find the object deformations and forces.

The discretisation adopted by the method, based on the long elements, has two main advantages: the number of elements used to fill an object is one order of magnitude less than in a discretisation based on tetrahedric or cubic elements; the graphic and the haptic feedback can be directly derived from the elements, and no intermediate geometric representation is needed. The use of static instead of PDE equations avoids all the problems concerning numerical integration, ensuring stability for the simulation.

No pre-calculations or condensations are used, in order to enable real time topology changes. The idea is to fill the volume with long elements, to define equilibrium equations for each element based on the stated principles and to add global constraints in order to obtain a global physical behavior.

Different meshing strategies can be conceived to fill the objects. We use Cartesian meshes. The long elements are parallel to the Cartesian axis and cross the object. One mesh defines one deformable face for the object. Multiple meshes can be combined to obtain a full 3D deformable object.

A long element can be compared to a non-linear spring fixed in one extremity and having the other extremity attached to a point in the movable object surface. These springs are relaxed when the solid is not touched (not deformed). The spring constant depends on its length. A long element does not occupy real space and has no mass. The real space inside the solid is occupied by some incompressible fluid with mass (density).

To re-establish the only one entry solid, two border conditions are applied:

• Pascal’s principle says that an external pressure applied to a fluid confined within a closed container is transmitted undiminished throughout the entire fluid
• The fluid is considered incompressible. It means that the volume conservation must be guaranteed when there is some external contact to the object. The volume dislocated by the contact will cause the dislocation of the entire surface, or in other words, the variation of volume due to the elements touched by the contact have to be equal to the sum of the volume created by the dislocation of all untouched elements to ensure the volume conservation.

LEM was used to implement a generic soft tissue VR simulator. The simulator was implemented in C++ in a Windows NT platform. The system main modules are:

• Model definition: the geometry and the physics of the objects to be simulated are defined using available information. This information can be derived from segmented real data or from intermediate models. The volumes are meshed to define the long elements
• Simulation loop: solves the system equations to obtain the deformed shape of the objects
• Rendering loops: graphic and haptic loops enable the interaction with the objects.

In a standard dual 700MHz PC one iteration of the simulation loop takes about 0.05 seconds for a 600 elements mesh. Note that a given discretisation in our method gives far more precise deformations than the same number of tetrahedra or cubes in a standard mesh. The global deformations are physically consistent and important phenomena such as the movement of all parts of the solid due to the preservation of volume are automatically produced. The method presented in this paper is intended for being part of a more general VR simulator. The method solves the deformation problem in an elegant and simple way, independently of other simulation aspects as movements (translation, rotation, dynamics integration, etc), topology changes and collision handling. To obtain a generic simulator the LEM must be integrated to methods suitable to handle these aspects. To add movements to the simulated objects we intend to implement a skeleton-like structure inside the object and to base the dynamics estimation on it. Larges deformations, as twisting and bending will be then possible.

To facilitate modelling and collision detection we intend to couple the LEM to implicit or parametric surface methods. The deformations of the model will be simulated in a set of LE meshes defining deformable 2D sheets and rendered as a 3D volume through an implicit of parametric formulation of the object shape.

The transformation from 2D sheets to 3D surfaces can be done using texture mapping techniques. Topology changes are typically task-oriented and use task-specific interfaces. We intend to implement a surgical interface based on medical procedures (cutting, suturing, removing material, etc).

The method can also be useful to validate and to adjust estimated biomechanical parameters in biologic tissues. Experimental data can be compared to simulation results.

The project is carried out among the SHARP research groups at INRIA, CATSS-Stanford University-USA and Catholic University of Brasilia-Brazil.

Links:
Sharp Research Group at INRIA: http://www.inrialpes.fr/sharp
CATSS-Stanford University, USA: http://www.catss.stanford.edu

Please contact:
Ivan F. Costa - INRIA and Catholic University of Brasilia
Tel: +55 61 356 9000
E-mail: ivan-ferreira.costa@inrialpes.fr

Remis Balaniuk - CATSS-Stanford, University and University of Brasilia
Tel: +1 650 724 7397
E-mail: remis@robotics.stanford.edu