
ERCIM News No.44 - January 2001 [contents]

![]()
ERCIM News No.44 - January 2001 [contents]
by Philippe Baptiste
For a long time, Operations Research and Artificial Intelligence could be seen as alternative approaches to solve real life optimisation problems such as scheduling or resource allocation. It now seems clear that we can have the best of both worlds by some hybrid techniques embeded in a constraint programming framework.
Scheduling, that can be defined as the process of allocating scarce resources to activities over a period of time, is the key point of many industrial problems. ‘Good’ schedules enable to make better decisions about how to commit resources, including equipment, capital, people, vehicles, facilities, etc. The problem of scheduling activities is a discrete optimization problem and therefore very hard to solve in practice (most of the scheduling problems are NP-Hard). To find good solutions or even solutions that meet all constraints, one has to explore a gigantic search space, most often exponential with the size of the problem. Because a brutal exploration of the search space is not possible, several techniques have been proposed in the past forty years, including Mixed Integer Linear Programming, Branch-and-Bound or more recently Constraint Programming.
Constraint programming is concerned with solving instances of the Constraint Satisfaction Problem (CSP). Informally speaking, an instance of the CSP is described by a set of variables, a set of possible values (domain) for each variable, and a set of constraints between the variables. The question is whether there exists an assignment of values to variables, so that all the constraints are satisfied. The interest of this technique lies in using constraints to reduce the computational effort needed to solve combinatorial problems. Constraints are used not only to test the validity of a solution, as in conventional programming languages, but also in a constructive mode to deduce new constraints and rapidly detect inconsistencies.
Fo
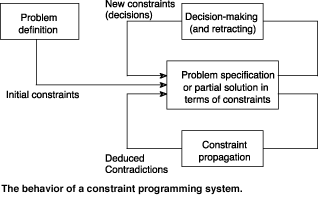
For complexity reasons, constraint propagation is usually incomplete. This means that some but not all the consequences of constraints are deduced. In particular, constraint propagation cannot detect all inconsistencies. Consequently, tree search algorithms must be implemented to determine if the CSP instance is consistent or not. The overall behavior of a constraint-based system is depicted on the Figure. The figure underlines the fact that problem definition, constraint propagation and decision making are clearly separated:
The separation between constraint propagation and the other parts of the system is a key feature of constraint programming. It impacts a lot on the reusability of the constraint propagation algorithms in the several applications where similar constraints apply. This explains the success of commercial and public domain constraint programming packages such as ILOG SOLVER, CHIP, ECLIPSE, CLAIRE and ECLAIR.
The efficiency of constraint based scheduling applications could be drastically improved by using dedicated operations research techniques: On the one hand operations research offers efficient algorithms to solve problems that however might not be well suited to be used in practice, and on the other hand constraint programming offers algorithms that are more generally applicable, but that might suffer from somewhat poor performance. It now seems clear that the best of both worlds, ie, efficient algorithms that can be applied apply to a wide range of problems, can be reached by hybrid techniques. Following this idea, very good results have been obtained on several industrial applications such as Staff Planning, Vehicle Production Optimization or Job-Shop Scheduling.
Please contact:
Philippe Baptiste - CNRS, Compiègne University of Technology
Tel: +33 3 4423 4952
E-mail: Philippe.Baptiste@hds.utc.fr
http://www.hds.utc.fr/~baptiste