
by Anna Bernasconi and Alberto M. Segre
A new technique for ab initio protein structure prediction, based on Ramachandran plots, is currently being studied at the University of Iowa, under the guidance of Prof. Alberto M. Segre, in collaboration with the Institute for Computational Mathematics, IMC-CNR, Pisa.
One of the most important open problems in molecular biology is the prediction of the spatial conformation of a protein from its primary structure, ie from its sequence of amino acids. The classical methods for structure analysis of proteins are X-ray crystallography and nuclear magnetic resonance (NMR). Unfortunately, these techniques are expensive and can take a long time (sometimes more than a year). On the other hand, the sequencing of proteins is relatively fast, simple, and inexpensive. As a result, there is a large gap between the number of known protein sequences and the number of known three-dimensional protein structures. This gap has grown over the past decade (and is expected to keep growing) as a result of the various genome projects worldwide. Thus, computational methods which may give some indication of structure and/or function of proteins are becoming increasingly important. Unfortunately, since it was discovered that proteins are capable of folding into their unique native state without any additional genetic mechanisms, over 25 years of effort has been expended on the determination of the three-dimensional structure from the sequence alone, without further experimental data. Despite the amount of effort, the protein folding problem remains largely unsolved and is therefore one of the most fundamental unsolved problems in computational molecular biology today.
How can the native state of a protein be predicted (either the exact or the approximate overall fold)? There are three major approaches to this problem: ‘comparative modelling’, ‘threading’, and ‘ab initio prediction’. Comparative modelling exploits the fact that evolutionarily related proteins with similar sequences, as measured by the percentage of identical residues at each position based on an optimal structural superposition, often have similar structures. For example, two sequences that have just 25% sequence identity usually have the same overall fold. Threading methods compare a target sequence against a library of structural templates, producing a list of scores. The scores are then ranked and the fold with the best score is assumed to be the one adopted by the sequence. Finally, the ab initio prediction methods consist in modelling all the energetics involved in the process of folding, and then in finding the structure with lowest free energy. This approach is based on the ‘thermodynamic hypothesis’, which states that the native structure of a protein is the one for which the free energy achieves the global minimum. While ab initio prediction is clearly the most difficult, it is arguably the most useful approach.


There are two components to ab initio prediction: devising a scoring (ie, energy) function that can distinguish between correct (native or native-like) structures from incorrect ones, and a search method to explore the conformational space. In many methods, the two components are coupled together such that a search function drives, and is driven by, the scoring function to find native-like structures. Unfortunately, this direct approach is not really useful in practice, both due to the difficulty of formulating an adequate scoring function and to the formidable computational effort required to solve it. To see why this is so, note that any fully-descriptive energy function must consider interactions between all pairs of atoms in the polypeptide chain, and the number of such pairs grows exponentially with the number of amino acids in the protein. To make matters worse, a full model would also have to contend with vitally important interactions between the protein’s atoms and the environment, the so-called ‘hydrophobic effect’. Thus, in order to make the computation practical, simplifying assumptions must necessarily be made.
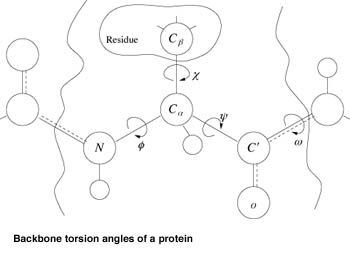
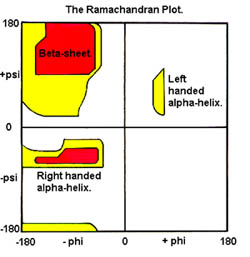
Different computational approaches to the problem differ as to which assumptions are made. A possible approach, based on the discretization of the conformational space, is that of deriving a protein-centric lattice, by allowing the backbone torsion angles, phi, psi, and omega, to take only a discrete set of values for each different residue type. Under biological conditions, the bond lengths and bond angles are fairly rigid. Therefore, the internal torsion angles along the protein backbone determine the main features of the final geometric shape of the folded protein. Furthermore, one can assume that each of the torsion angles is restricted to a small, finite set of values for each different residue type. As a matter of fact, not all torsion angles are created equally. While they may feasibly take any value from -180 to 180 degrees, in nature all these values do not occur with uniform probability. This is due to the geometric constraints from neighboring atoms, which dramatically restrict the commonly occurring legal values for the torsion angles. In particular, the peptide bond is rigid (and shorter than expected) because of the partial double-bond character of the CO-NH bond. Hence the torsion angle omega around this bond generally occurs in only two conformations: ‘cis’ (omega about 0 degrees) and ‘trans’ (omega about 180 degrees), with the trans conformation being by far the more common. Moreover the other two torsion angles, phi and psi, are highly constrained, as noted by G. N. Ramachandran (1968). The (paired) values allowed for them can be selected using clustering algorithms operating in a Ramachandran plot space constructed from the protein database (http://www.rcsb.org/pdb), while discrete values for omega can be set to {0,180}. This defines a space of (2k)n possible conformations for a protein with n amino acids (assuming each phi and psi pair is allowed to assume k distinct values). In this way, the conformational space of proteins is discretized in a protein-centric fashion. An approximate folding is then found by searching this reduced, discrete space, guided by some scoring function. Of course, this discrete search process is an exponential one, meaning that in its most naive form it is impractical for all but the smallest proteins. Thus, the search should be made more palatable by incorporating a number of search pruning and reduction techniques, and/or by exploring the discrete space in parallel. From this naive folding, appropriate constraints (based on atomic bonds present, their bond lengths, and any Van der Waals or sulfide-sulfide interactions in the naive folding) are derived for an interior-point optimization process, which adjusts atomic positions and computes an energy value for this conformation. The computed energy value is then passed back to the discrete space and used to tune the scoring function for further additional parallel pruning.
Please contact:
Anna Bernasconi - IMC-CNR
Tel. +39 050 3152411
E-mail: bernasconi@imc.pi.cnr
or Alberto M. Segre - University of Iowa
E-mail: alberto-segre@uiowa.edu