
by Thierry Fraichard
As part of an effort to design an autonomous car-like vehicle, the Sharp research group at INRIA Rhône-Alpes develops new motion planning techniques that take into account the various constraints that restricts the motion capabilities of such a vehicle (kinematics, dynamics, uncertainty).
Motion planning deals with the a priori computation of the motion that is to be executed by a robotic system. In its basic form, motion planning addresses primarily collision avoidance with the stationary obstacles of the environment. However, when the robotic system considered is a car-like vehicle, there is much more to motion planning than that. For a start, such a vehicle is subject to kinematic and dynamic constraints that restricts its motion capabilities. Then it moves among moving obstacles that should be avoided too. Finally, it is affected by various sources of uncertainty (control, sensing and model errors), that may lead to failure at execution time.
Configuration space is the fundamental tool introduced in the late seventies to address the basic motion planning problem. The configuration of a robot is a set of parametres representing the position and orientation of every part of the robot. In its configuration space, a robot is represented as a point, stationary obstacles are represented as forbidden regions and motion planning is reduced to finding a path, ie a continuous sequence of configurations, that avoids the forbidden regions. When time-dependent constraints such as moving obstacles and robot dynamics are considered, it is necessary to plan a trajectory, ie a path parameterized by time. Configuration space does not permit to take into account time-dependent constraints.
Our first contribution has been to introduce state-time space as a tool to deal with time-dependent constraints. The state-time space of a robot is its state space, ie the space of the configuration parametres and their derivatives, augmented of the time dimension. In this framework, the constraints imposed by both the moving obstacles and the robot dynamics can be represented by static forbidden regions of state-time space. A trajectory maps to a curve in state-time space and motion planning can be reduced to finding a curve that avoids the forbidden regions. Such a curve must respect additional constraints due to the fact that time is irreversible and that velocity and acceleration constraints translate to geometric constraints on the slope and the curvature along the time dimension. However, it is possible to extend existing methods for path planning in configuration space in order to solve the problem at hand. In particular, we developed a general approach to solve motion planning problems formulated in the state-time space framework. The approach places a regular grid in state-time space and searches the grid for a trajectory using dynamic programming.
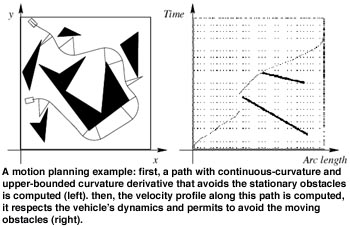
The environment of a car-like vehicle is structured, it can be viewed as a network of roadlanes. We decided to take advantage of this structure in order to reduce the overall complexity of motion planning by decomposing it into two complementary stages of lesser complexity: (1) planning a path avoiding the stationary obstacles, and (2) planning the velocity along this path so as to avoid the moving obstacles. The velocity planning stage deals with the time-dependent constraints, namely the moving obstacles and the vehicle’s dynamics. It applies the state-time space approach presented above. The time-independent constraints are taken into account in the path planning stage: its purpose is to compute a path that avoids the stationary obstacles and respects the vehicle’s kinematic constraints.
A car-like vehicle is a nonholonomic system: it is subject to kinematic constraints that restricts its admissible directions of motion. Thus it can only move forward or backward in a direction perpendicular to the orientation of its rear wheels axle; besides its turning radius is lower bounded (because of the mechanical limits on the steering angle).
Nonholonomy appeared in path planning in the mid-eighties and a lot of results have been obtained since. For car-like vehicles, most of the existing works compute paths made up of line segments connected with tangential circular arcs of minimum radius. One reason for this choice is that the shortest path between two configurations for a car-like vehicle is such a path. However the curvature of this type of path is discontinuous: discontinuities occur at the transitions between segments and arcs. The curvature is directly related to the orientation of the front wheels of the car. Accordingly, if a car were to track precisely such a type of path, it would have to stop at each curvature discontinuity so as to reorient its front wheels. It is therefore desirable to plan continuous-curvature paths. Besides, since the derivative of the curvature is directly related to the steering velocity of the car, it is also desirable that the derivative of the curvature be upper-bounded.
Our main contribution here has been to propose one of the first algorithms that compute collision-free paths with continuous-curvature and upper-bounded curvature derivative for car-like vehicles. The paths computed are made up of line segments and circular arcs connected by clothoids, ie curves whose curvature varies linearly with their arc length. They are locally optimal and it is conjectured that they are globally suboptimal, ie longer than the optimal paths of no more than a given constant. Experiments carried out with a real car have demonstrated the superiority, in terms of tracking precision, of this type of paths.
The underlying assumption of the trajectory planning technique presented above (and of most of the existing ones for that matter), is that the vehicle should be able to follow the trajectory accurately enough. A challenging problem is that this assumption hardly holds for a real vehicle operating in the real world. To begin with, such vehicles usually rely on odometry to estimate their configuration. As these techniques yield increasing and unbounded configuration uncertainty, failure to follow a planned trajectory is bound to occur. To overcome this problem, the vehicles are often equipped with absolute localization devices. These devices usually rely on sensors identifying environmental features that are then matched against a priori models of the environment in order to estimate the vehicle’s configuration. However if a planned trajectory does not allow the detection of the appropriate environmental features, the vehicle may once again fail to reach its goal. A solution to these two problems (drift, feature detection), both related to the various sources of uncertainty affecting the vehicle, is to explicitly take into account uncertainty so as to compute safe trajectories, ie trajectories that guarantee that the goal will be reached in spite of these uncertainties.

We have developed a safe motion planner for a car-like vehicle that estimates its configuration with odometry and an absolute localization device based on environmental feature matching. Our solution relies upon: (a) simulations of the vehicle’s odometry and feature matching localization procedure in order to estimate in a conservative way how the configuration uncertainty evolves when the vehicles moves or localizes itself, and (b) a novel type of landmarks characterized by: (1) a region of the configuration space, (2) a set of best features for localization in the region, and (3) a perception uncertainty field that measures how well a given feature is perceived at each configuration in the region. The landmarks are built automatically, they simplify and improve localization. The solution algorithm uses a roadmap, ie a graph in the configuration space whose edges are collision-free paths that respects the nonholonomic constraints of a car-like vehicle. The roadmap is searched for the shortest path to the goal. Safeness along each edge-path is checked thanks to the odometry simulation. Whenever a node included in a landmark region is reached, feature matching localization takes place and configuration uncertainty is reduced accordingly. The algorithm returns a motion plan that alternates motions along safe paths and localization operations.
Future activities are aimed at improving and extending the different techniques presented above, and mainly at integrating them inside a single motion planner.
This work was carried out in the framework of a number of European and French research programmes focused on the development of novel road transport technologies: Prometheus, Praxitèle and La Route Automatisée.
Links:
Sharp: http://www.inria.fr/Equipes/SHARP-eng.html
Prometheus:http://www3.eureka.be/home/
Praxitèle: http://www-rocq.inria.fr/praxitele/
La Route Automatisée: http://www.lara.prd.fr/
Thierry Fraichard’s home page: http://www.inrialpes.fr/sharp/people/frchard/
Please contact:
Thierry Fraichard - INRIA Rhône-Alpes
Tel: +33 4 76 61 52 21
E-mail: thierry.fraichard@inria.fr