
by Stanislav Saic and Josef JeÏek
The progress made in computer technology during the recent years allows to solve more difficult tasks also in the field of geoscience. Many new results can be obtained by reconsidering old mathematical/ numerical solutions and using powerful computers. A typical example is the three dimensional dymamical modelling of rigid objects moving in viscous fluid and the flow around them.
In ductile shear zones and in metamorphic rocks in general, the geometry of fabrics of rocks is a valuable source of information on the kinematics and dynamics of flow. In order to understand the fabric development, structural geologists use numerical or analogue modelling of the behaviour of rigid objects embedded in a viscous matrix. Numerical models are based on continuum mechanics and, with more or less accuracy, describe the motion of a rigid body and/or the flow around it.
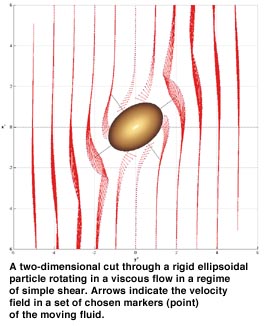
A pioneering work in this domain was carried out by G.B. Jeffery in 1922, who developed equations of the rotation of an isolated rigid ellipsoidal particle in a slowly moving Newtonian viscous fluid. Analytical or numerical integration of these equations give the trajectory of a particle in a flow described by a velocity gradient tensor. Jeffery’s work has been broadly used and discussed by those who studied the development of shape-preferred orientation in rocks. Jeffery also developed equations that can be used for numerical evaluation of the surrounding velocity field. It is surprising that the equations have not been used for this purpose up to nowadays. The possible reasons are a rather complicated procedure of development, the need for an efficient algorithm for the numerical evaluation of elliptic integrals in Jeffery’s formulas and a possibility of computer implementation of the whole problem. Moreover, the original manuscript of Jeffery contained some errors (most probably misprints) that did not affect the equations of rotation of the inclusion, but significantly affected those for the surrounding velocity field. We present a procedure based on the equations of Jeffery that were re-developed and corrected. We found an efficient way to compute the elliptic integrals that are needed for the solution and produced software for computer modelling and visualisation of the problem. In the set of three figures we demonstrate a result of modelling with an application to structural geology.

The porphyroblast is approximated by a growing ellipsoidal inclusion rotating around its longest axis parallel to the rotation axis of simple shear. Markers representing external foliations were initially arranged in lines and moved with the viscous fluid until they were captured by the growing porphyroblast.
We conclude that, in comparison to recently used procedures, the procedure and computer program we have developed represent a fully three-dimensional hydrodynamical model. It permits considering ellipsoidal inclusions and a general type of flow, and therefore to study how the asymmetry of the inclusion and different kinematic conditions influence flow patterns and structures around rigid objects in a ductile matrix.
The research was supported by the Grant Agency of the Czech Republic under Grant No. 102/96/0419.
Please contact:
Stanislav Saic - CRCIM
Tel: +420 2 6605 2211
E-mail: ssaic@utia.cas.cz