Statistics of Hidden Markov Models

by François Le Gland

---

Hidden Markov models (HMM) are a special case of partially observed dynamical systems, where the state of a finite Markov chain should be estimated from a sequence of noisy observations. This article gives an overview of some progress made recently in the SIGMA2 research group at INRIA Rennes / IRISA, in the identification of general HMM’s and in the design of approximation methods for continuous state HMM’s, which have attracted a lot of interest recently under the generic name of particle filtering.

Hidden Markov models (HMM) are widely used in speech recognition, biological sequences alignment, etc. These models are a special case of partially observed dynamical systems, where the state of a finite Markov chain should be estimated from a sequence of noisy observations.

A related problem, in which significant progress has been made recently, is to identify the model from observations. It is easy to express the log-likelihood function, the conditional least squares error and other classical statistics, in terms of the prediction filter, which is the probability distribution of the state given past observations. Similarly, the score function and the conditional least squares residual can be expressed in terms of the gradient of the prediction filter with respect to the unknown parameter.

Our main contribution has been to introduce the extended Markov chain consisting of the unobserved state, the observation, the prediction filter and its gradient, and to prove the existence of a unique invariant probability distribution for this chain, from which the law of large numbers and the central limit theorem can be proved. For a wide class of minimum contrast estimators, including the maximum likelihood estimator and the conditional least squares estimator, it is then easy to prove consistency, i.e. convergence to the set of maxima of the associated contrast function, and asymptotic normality, as the number of observations tends to infinity. We have obtained similar convergence results for the Bayesian estimator and for recursive versions of the estimators. Part of this work is the result of a co-operation with members of the ERCIM working group on Control and System Theory: Lorenzo Finesso (CNR-LADSEB), Lászlo Gerencsér (SZTAKI) and György Michaletzky (Eötvös Loránd University).

Future activities will be devoted to extending the same approach to more general models, with emphasis on:

• distributed discrete events dynamical systems, such as those introduced by Eric Fabre for fault diagnosis in tele-communication networks (see page 31 in this issue)
• hidden Markov models with continuous state space.

Extension to continuous state space immediately raises the question of computing the prediction filter, even approximately. An attractive answer to this question has been proposed recently, under the generic name of particle filtering, in which the prediction filter is approximated in terms of the empirical distribution of a particle system. The particles move independently according to the state equation, and whenever a new observation is available, resampling occurs in which the particles are selected according to their consistency with the observation (as measured by the likelihood function). The positive effect of the resampling step is to automatically concentrate particles in regions of interest of the state space. The method is very easy to implement, even in high dimensional problems, since it is sufficient in principle to simulate independent sample paths of the hidden dynamical system, and it allows also for parallel implementation, eg on a cluster of workstations or PC’s.

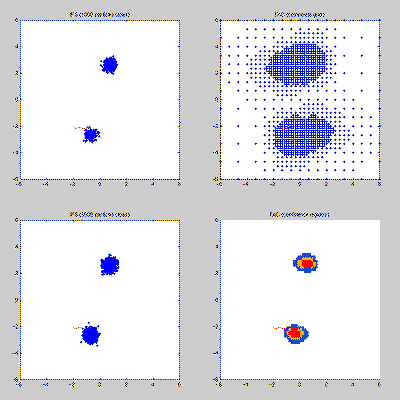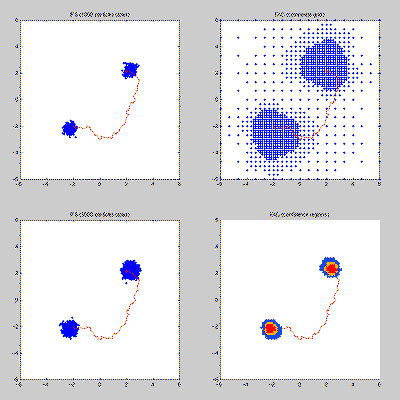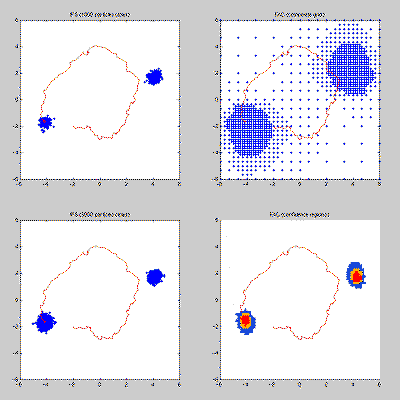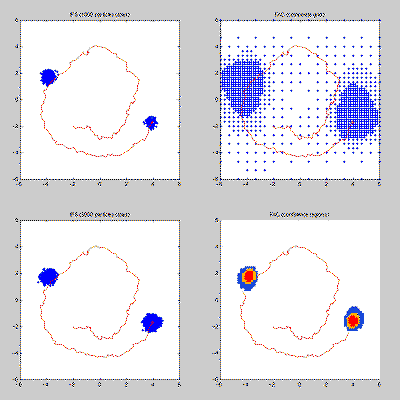
Figure: Both the particle filter (left column) and a multigrid method with locally refined adaptive grid (right column) have the ability to concentrate the computing effort in relevant regions of the state space. In terms of the programming effort however, the particle filter is much cheaper.

Our contribution has been to propose modifications of the original method, so as to handle efficiently the (difficult) case where the state and / or observation noise are small. One approach is to regularize the empirical distribution associated with the particle system, using a kernel method.

Another approach is based on the progressive correction principle, in which the correction step is splitted into subcorrection steps associated with a decreasing sequence of (fictitious) variance matrices for the observation noise. These improved particle methods have been applied successfully to various target tracking problems.

This work is the result of a co-operation with Christian Musso and Nadia Oudjane (ONERA/DTIM/MCT), and has benefited from the support of CNRS, through a research project co-ordinated by Pierre Del Moral (Université Paul Sabatier).

Links:

SIGMA2 research team: http://www.irisa.fr/sigma2/index-en.html

Please contact:

François Le Gland - INRIA Rennes / IRISA
Tel: +33 2 99 84 73 62
E-mail: legland@irisa.fr