Optimal Control of Distributed Parameter Systems
by Jaroslav Haslinger, Michal Kocvara, and Tomás Roubícek
Control of systems can be performed directly in open loops in such a way that a certain criterium attains its optimal value. Typical examples of such criteria are cost, consumed energy, or total time to be minimized.
The controlled system arising in engineering practice, physics, medicine, etc., often must be considered with distributed parameters, being then governed typically by partial differential equations or/and integral equations. Even more, sometimes the system may be governed by inequalities of this sort; this happens typically in various contact problems in mechanics. The variety of optimization problems governed by DPSs (distributed parameter systems) includes not only classic optimal control problems, but also optimization of the shape (so-called optimal shape design) and optimization of coefficients (so-called identification problem or material optimization).
Tools used for optimal control of DPSs varies from purely theoretical as mathematical analysis (nonlinear, (non)convex, nonsmooth analysis) and theory of nonlinear partial differential equations, through numerical as finite element methods and optimization algorithms, to application oriented tools, including computer implementation, visualization, and a certain knowledge of the background of concrete problems in questions.
This sort of research has been performed for decades on academic ground by two of Prague’s CRCIM members: The Institute of Information Theory and Automation of the Academy of Sciences and the Faculty of Mathematics and Physics of the Charles University. Before the fall of communism, this community had various collaborations with Czech steel industry, mainly through the Skoda factory. The problems covered optimal control of heating of large parts of pressure tanks of nuclear reactors, identification of parameters and shape optimal design in casting devices, etc. This collaboration, however, finished soon after 1989 during a re-structuring of the Czech heavy industry. But decay of industrial research in the Czech Republic has been far compensated by the possibility to open new contacts with academic institutions worldwide. In Europe, Prague’s DPS-optimal-control group keeps regular collaboration particularly with scientists from Germany, France and Finland. Other contacts are maintained, eg, within IFIP Working Group 7.2 ‘Computational Techniques in Distributed Systems’.
Presently, this (rather small) research group confines to academic problems to maintain this sort of knowledge in Czech Republic for expected future re-establishment of industrial collaborations within European community. One of fields of our current interest is shape optimization, formulated in a classical way as a design of stressed structures in mutual contact involving possibly friction effects on common surfaces. Since the state problem is modelled by a variational inequality, the optimization problem becomes non-smooth, meaning that the control-state relation is non-differentiable, in general. This fact excludes (or at least complicates) the usage of classic gradient type methods. We are further interested in developing new computational methods in shape optimization such as fictitious domain solvers in combination with derivative free minimization methods.
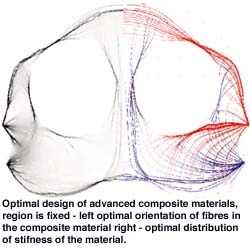
Apart from classic shape optimization, the group is also interested in optimization of material distribution and material properties. The latter is closely connected with design of advanced composite materials used, eg, in car and aircraft industry. Efficiency of this approach relies on fast numerical optimization methods, like interior point and barrier algorithms, that can handle systems with hundreds of thousands of unknowns. Typical application of the approach in the so-called conceptual design is presented in the figure.
Great attention is paid to optimization of fine structures arising in various physical systems due to the nonconvexity of governing potentials. This gives rise to multiscale problems which are extremely difficult to model on computers and which represent a great challenge for numerics for next century. Yet, certain effective algorithms to model such microstructures on a ‘mesoscopical’ level have been developed and tested by Prague’s group, while optimal control or design of such microstructures has been investigated so far rather on theoretical level. Our applications included micromagnetism in ferromagnetic materials and matrensitic microstructures in shape-memory alloys. Let us emphasize that such ‘smart materials’ already find broad and sophisticated applications in engineering and medicine, and their optimization will become interesting in close future.
Please contact:
Jaroslav Haslinger - CRCIM
Tel: +420 2 2191 1312
E-mail: haslin@apollo.karlov.mff.cuni.cz