Solving Implicit Differential Equations within a Modeling Environment
by Jacques de Swart
Many industrial applications can be modeled by sets of Implicit Differential
Equations (IDEs). In joint work at CWI and Paragon Decision Technology
(PDT), sponsored by the Technology Foundation STW, it is shown
how the integration of an IDE solver in an algebraic modeling
system can help to overcome many of the difficulties that a user
currently encounters in trying to solve such systems of IDEs.
In industrial design processes, testing designs is of major importance.
Before products are manufactured based on some design, one wants
to know how a product based on this design would behave under
several circumstances. For this purpose, one models the product
in terms of its design. By solving the model, one simulates the
working of the product. This procedure is much cheaper than building
and testing prototypes. Often the modeling of a product results
in IDEs – equations in which derivatives of the unknowns with
respect to one independent variable, typically time, appear implicitly.
The modeling of time-dependent processes often results in IDEs.
To solve IDEs, numerical methods are indispensable.
Examples of applications where simulation processes involve IDEs
are testing the design of an electrical circuit, and the formulation
of safety requirements for trains. Other areas include the modeling
of turbulent flows in water tube systems, the description of demand-supply
curves in liberalized markets, and the simulation of chemical
reactions.
On the one hand, the complexity and size of the applications require
a user friendly modeling environment, which speaks the language
of the modeler, and offers the possibility to test and compare
several scenarios and instances of the model data efficiently.
Moreover, the modeler does not want to be involved in the often
cumbersome interfacing with solvers. On the other hand, modern
numerical techniques are required to solve ill-conditioned IDE
systems of high dimension. How to meet these requirements is studied
by integrating the novel IDE solver PSIDE, developed at CWI, in
the advanced modeling environment AIMMS (Advanced Interactive
Multi-dimensional Modeling System), which is a product of PDT.
If the time scales of the various solution components vary greatly,
and if the rapidly changing components are physically irrelevant,
then we call a problem stiff. For example, if both high and low
frequency signals are present in an electrical circuit, but the
high-frequent signals are small in magnitude, then the modeling
of such a circuit gives rise to a stiff system of IDEs. To solve
such IDEs, an implicit method is required, which means that the
numerical approximations are not directly available, but have
to be computed from nonlinear systems. This computation requires
the evaluation of Jacobians of the IDEs with respect to the unknowns.
In AIMMS these Jacobians are available in analytical form.
If some solution components of an IDE are more sensitive to perturbations
than others, then the IDE is said to be of higher index. In order
to integrate IDEs numerically with variable stepsize, one usually
estimates a local error , in which the index has to be taken into
account. Existing IDE solvers do not have a facility to compute
the index. An automatic index determination facility for PSIDE,
which uses the analytical Jacobian available in AIMMS, is currently
under development.
The IDE solver has to know not only the values of all variables
at the start of the integration interval, but also their derivatives.
Especially the latter are in practice often unknown to the modeler
and have to be computed from an - often nonlinear - system of
algebraic equations. A powerful commercial nonlinear solver available
in AIMMS is CONOPT. We used CONOPT successfully to compute the
missing initial values. For higher index problems the problem
of finding initial values is even more complicated, because the
initial values have to satisfy differentiated equations as well.
Based on the index determination facility and the capability of
AIMMS to differentiate equations automatically, we are working
on an automatic procedure for finding initial values for higher
index problems.
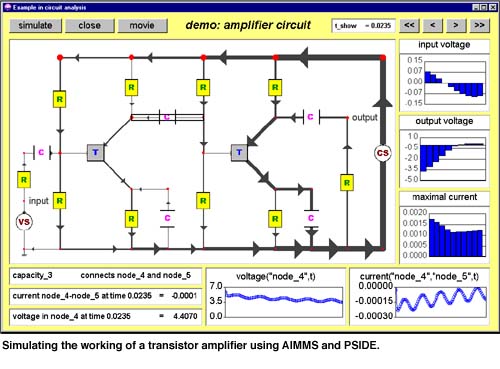
One problem in the CWI Test Set is the Transistor Amplifier, whose
circuit diagram is shown in the Figure. The task is to compute
the behaviour of the voltages in the nodes and the currents in
the wires over time. There are several symbolic equations, such
as Kirchoff&Mac226;s Law, whereas for every type of electrical component there is
an equation describing its working. These equations are independent
of the specific electrical circuit. To simulate another circuit
one only has to adapt model data. The application shown in the
figure is clickable. One can play the movie of the circuit&Mac226;s working and select the wires and nodes of which one wants to
see more information. As additional information, the maximum of
the currents over all wires is displayed. The ‘<<’, ‘<’, ‘>’ and
‘>>’ buttons serve to step through the movie.
Please contact:
Jacques de Swart - CWI/PDT
Tel: +31 20 592 4176
E-mail: jacques@cwi.nl, Jacques.de.Swart@paragon.nl
