ERCIM News No.36 - January 1999

Formal Underpinnings of Object Technology

by Juan Bicarregui

---

Object-Oriented Analysis and Design notations, such as UML, are rapidly becoming the mainstream industrial approach to the development of software. They include a range of techniques for a wide spectrum of software engineering tasks from domain modelling to implementation. However, such techniques are generally without a formal interpretation which is essential for rigorous development as required by applications in critical areas, such as medical database and robotic systems, defence and chemical process control.

In collaboration with Imperial College, London, and Brighton University, we are developing a compositional formal interpretation of object model and statechart diagrams as used in OOA\&D notations. We interpret diagrams as logical theories in the Object Calculus (Fiadeiro and Maibaum 1991). Separate theories are constructed for separate diagram components such as object instances, class managers and associations which are then combined with categorical constructions to yield a modular definition of a whole system.

For example, the interpretation of an object class is constructed by taking the co-limit of theories for instances of the class and a general manager theory which handles the creation and deletion of instances. Associations are interpreted by bringing together the theories of the associated classes with a general theory for associations via link theories that ‘glue’ the identifiers of the associated theories with that of a generic association. Annotations such as cardinality or aggregation constraints are interpreted as axioms in the co-limit theory. In this framework, aggregation and subtyping can be seen as special cases of the general concept of association.

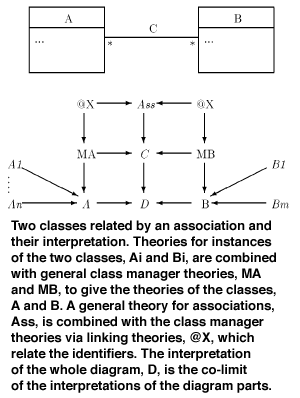
The Object Calculus defines a notion of locality which ensures that only actions local to a particular theory can effect the value of the local attributes. Locality is a logical counterpart to object-oriented data encapsulation and the work has led us compare these two principles.

The formalisation has been used to justify some common transformations of class models such as those presented in the UML literature. By providing a semantically-based transformation calculus it is possible to obtain many of the benefits of formal methods without the need for users to reason directly in mathematical formalisms.

The incremental approach to the interpretation of diagrams makes the formalisation suitable as a basis for a support system which would provide a formal basis for the validation and verification of system specifications.

Please contact:

Juan Bicarregui - CLRC
Tel: +44 1235 44 6648
E-mail: jcb@inf.rl.ac.uk