Partial Differential Equations in Porous Media Research
by Hans van Duijn
Mathematical modelling of flow and transport through porous media plays an important role in environmental studies as well as in reservoir engineering. Applications include the spread of pollutants from a landfill through the soil system and of oil spills in the subsurface, the intrusion of salt seawater in coastal aquifers, and new methods for enhanced oil recovery and underground gas storage. At CWI several of such problems are studied, ranging from very applied to theoretical research.
Although already intensively studied in the past, transport phenomena in porous media still yield new and challenging mathematical problems in the field of nonlinear partial differential equations (PDEs), free boundary problems, and homogenization procedures. Moreover, detailed numerical studies are necessary to improve the prediction capacity of the related models. CWI's research focuses on the mathematical modelling of transport processes in the subsurface, and on the qualitative analysis and numerical study of the governing PDEs.
In the field of PDE research particular attention was given to systems consisting of a convection-diffusion equation coupled with an ordinary differential equation. A special case, modelling salt uptake by mangroves, involves non-local convection. In a collaboration with the University of Bonn the interface between fresh and salt groundwater in the presence of wells is studied. The interface appears as a free boundary in an elliptic problem in which, depending on the pumping rate of the wells, a cusp singularity develops. In the case of heterogeneous media the interface was studied numerically, using a moving mesh Finite Element Method. Knowledge of the behaviour of the interface is important, eg, to estimate in how far seawater intrudes in aquifers in the Dutch coastal area when drinking water is pumped out. This research was highlighted for example at a tele-conference 'Mathematics and environ-ment: problems related to water', an initiative of the European Mathematical Society, which was held last December simultaneously at three locations: Amsterdam, Madrid, and Venice.
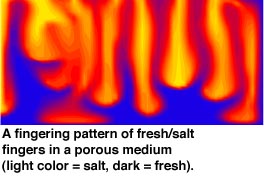 The study of density-driven flow in porous
media concentrates on brine transport problems related to high-level radio-active
waste disposal in salt domes. High salt concentrations give rise to non-linear
transport phenomena such as enhanced flow due to volume (compressibility)
effects and the reduction of hydrodynamical dispersion due to gravity forces.
A non-linear dispersion theory for this case, proposed by S.M. Hassanizadeh
(Delft University of Technology), was verified using experimental data
from the Technical University of Berlin.
The study of density-driven flow in porous
media concentrates on brine transport problems related to high-level radio-active
waste disposal in salt domes. High salt concentrations give rise to non-linear
transport phenomena such as enhanced flow due to volume (compressibility)
effects and the reduction of hydrodynamical dispersion due to gravity forces.
A non-linear dispersion theory for this case, proposed by S.M. Hassanizadeh
(Delft University of Technology), was verified using experimental data
from the Technical University of Berlin.
The pressure in active gas reservoirs in the Netherlands becomes insufficient to meet the needs during the winter period. Therefore Gas Unie/NAM (Nederlandse Aardolie Maatschappij) intends to store gas in depleted gas reservoirs which are no longer in production. These reservoirs act as a buffer to meet peak demand. In an ongoing project sponsored by NAM CWI studies gas injection into a reservoir, in order to understand and quantify the mixing (diffusion/ dispersion) of injected gas with residual gas in old reservoirs, and develops a numerical code to predict this mixing.
Another project concerns soil remediation techniques. Organic contaminants may be removed from the soil either by pumping methods or by injecting air (air sparging), which enhances biodegradation and volatilization. The corresponding flow of groundwater, organic contaminant and air is described using multi-phase flow models. For air injection into groundwater in a horizontally layered medium accurate numerical solutions of the full transient two-phase flow equations were found and an almost explicit solution for the steady-state air flow just below a less permeable soil layer was derived. To model pumping of a lens of light organic liquid from an aquifer, multi-phase seepage face conditions were applied at the well boundary. For two different geometries of the lens similarity solutions provided good approximations of the removal rate and the location of the remaining contaminant as a function of time.
Finally, in a recently started project PDE's with higher order mixed derivatives are studied. Such equations arise in models for unsaturated groundwater flow, taking into account dynamic capillary pressure.
See also : http://dbs.cwi.nl/cwwwi/owa/cwwwi.print_projects?ID=5
Please contact:
Hans van Duijn - CWI
Tel: +31 20 592 4208
E-mail: Hans.van.Duijn@cwi.nl
