The Use of Wavelets in Seismics and Geophysics
by Nico Temme
Wavelets are wave patterns of small size that can be used to analyze rapid changes in a signal, sharp contrasts in an image, and structures at different scales. The wavelet method, developed in the eighties and now provided with a sound mathematical basis, has become a powerful tool in the field of data compression, noise suppression and processing of images and signals. At CWI wavelets are studied in a project financed by the Technology Foundation STW which focuses on the application of wavelets in seismology and geophysics.
A wavelet is a wave-like function with short extension: its graph oscillates only over a short distance, or damps very fast; its mean value over the whole domain equals zero. A wavelet is localized both in frequency and position. From this 'mother wavelet' a whole family of other wavelets is derived by displacement and scaling. In this family every scale is represented for every wanted position. Wavelet analysis operates as a microscope: as a wavelet family contains 'building blocks' of arbitrary small scale, we may zoom in at any time on any detail of the signal. Wavelets are well suited to detect the presence of fractal components in observational data. As we observe images and acoustic signals mainly by contrasts, wavelets can be very effective in storing and transmitting such images and signals by data compression. Wavelets are also successfully applied for, eg, removing noise in old sound recordings and restoring images from MRI and CT scans.
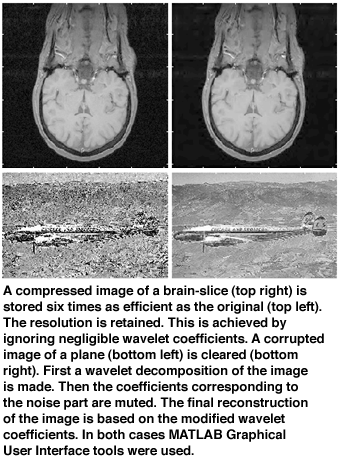Research on wavelets and its applications in The Netherlands takes place for instance at the Royal Dutch Meteorological Institute KNMI (structure of the clouds), Delft University of Technology (soil structures, for oil exploration), Groningen University (image processing in medicine) and CWI (analysis of geophysical/seismic signals). CWI's research is focused on the development and use of directional time-scale analysis methods.
An important research topic is the combination of the Radon transform (also called X-ray transform - a well-known technique for reconstructing a 3D object from a number of cross-sections) and the wavelet transform. A rigid mathematical formulation of this 'Wavelet X-ray Transform', its basic properties and its discretization have been obtained. A fast algorithm for this combined transform is also under development. The computer code has been established in a Matlab environment and the first results are promising.
The 'Wavelet X-ray Transform' is applied to the filtering of two-dimensional seismic data sets. These images contain information about the subsurface of the earth such as the localization of geological interfaces. However, they also contain irrelevant parts, for example contributions from waves coming directly from the explosion (that is used to generate the signals) to the detection point. CWI's wavelet method of filtering away the irrelevant parts prior to extraction of the relevant parameters is based on the idea that relevant and disturbing parts in an image can be separated based on distinction in position (or time), scale (or frequency) and direction.
Secondly, research is conducted jointly with KNMI on the problems of polarization in seismic signals, where an estimation of the spectrum is made by preprocessing the signal data. In a seismogram, the waves coming from the source and arriving at the Earth's surface at different arrival times appear as so-called phases. These phases, which can be seen as the ground motion due to the arrival of a particular wave coming from the source, are all measured during a short time period. A research aim is to find the time periods in a seismogram, when they appear. Furthermore we want to analyze these phases accurately.
Analysis of a short segment in a longer record by spectral estimation, ie, studying the frequency components of the Fourier spectrum, is hampered by the fact that its spectrum cannot be determined exactly if the data process is stochastic or a noisy deterministic signal.
A seismogram is a non-stationary data process and hence, instead of considering the Fourier spectrum, a direct estimate of the time-varying spectrum is more appropriate. For this we used the wavelet transform. Since at higher scales the wavelet transform too cannot deal with the uncertainty introduced by the short segment, we first preprocessed the segment with a tapering algorithm, which smoothes the data by multiplying the data segments with some window function, and then took the wavelet transform of the new data. The first mathematical results of our research contain error and convergence estimates of the new algorithm. Successful experiments with synthetic data will be followed by tests with real seismic data in collaboration with KNMI.
Other recently started research concerns the design of an algorithm based on the wavelet transform for the detection of time points, where the several phases appear in the seismogram. This is relevant for, eg, distinguishing a (nuclear) explosion from an earthquake and locating the source of the seismic event. Together with the seismology department of KNMI, physical properties of the seismic signals, especially their scaling behaviour, are used to refine the algorithm. See also http://www.cwi.nl/cwi/projects/wavelets.html
Please contact:
Nico Temme - CWI
Tel: +31 20 592 4240
E-mail: Nico.Temme@cwi.nl