Travelling Waves in Nonlinear Diffusion-Convection-Reaction Processes
by Róbert Kersner
Special solutions play an important role in the study of nonlinear partial differential equations (PDE's) arising in mathematical biology. Confronted with a mathematical model in the form of an initial or a boundary value problem for a partial differential equation or a system of such equations, the foremost desire of a practitioner is to solve the problem explicitly. If little theory is available and no explicit solutions are obtainable, generally the ensuing attack is to identify circumstances under which the complexity of the problem may be reduced. The study of these problems belongs to the main research directions of the Applied Mathematics Laboratory at SZTAKI.
In cooperation with the University of Twente, a technique has been developed for determining whether or not a nonlinear, possibly degenerate parabolic partial differential equation admits a travelling-wave (TW) solution, ie solution of the form f(x-ct) which does not change the shape f and where the speed c is constant. This technique is suitable for investigating properties of such travelling waves as well.
In ecological context, the different terms in such kind of partial differential equations represent the birth - death process, diffusion and convection. Typical examples for them are the Fisher or logistic equation, which is the archetypical deterministic model for the spread of an advantageous gene in a population of diploid individuals, the Nagumo equation, which models the transmission of electrical pulses in a nerve axon, and the Richards (or nonlinear Fokker-Planck) equation. Analogous systems of PDEs were proposed as models for the chemical basis of morphogenesis by Turing in 1952.
The principal contention of our method is that the study of the travelling wave solutions of partial differential equations above is equivalent to the study of the singular Volterra-type nonlinear integral equations in the following sense: the partial differential equation has a monotonic travelling wave solution connecting two states with a given speed if and only if the integral equation has a non-negative solution which is zero at these states.
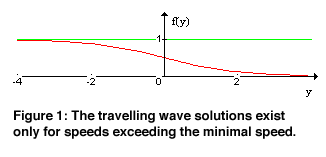
For the Fisher-type equations a typical result is that the travelling wave solutions exist only for speeds which are bigger than the minimal speed and have the form given in Figure 1. The minimal speed is an unknown of the problem, having great practical importance. In many cases, after some time the general process moves with this velocity.
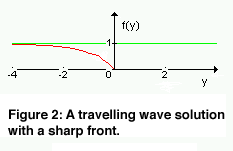
It may happen that a travelling wave solution has a sharp front (see Figure 2). This is the case, for example, for the generalised Fischer-type model, when the density dependence of the diffusion coefficient is power-like. The travelling wave solutions with not minimal speed have no sharp front (see Figure 1), but the unique wave with minimal speed has (see Figure 2). Note that this travelling wave has attractor property: after some time all the solutions of the original partial differential equation with initial data from a given class will take the form and the speed of this wave. Using the above mentioned integral equation method one can obtain these kind of results almost algorithmically, together with good estimates for the minimal speed.
Our developed technique provides an alternative to phase-plane analysis and has several advantages with respect to this classical approach. Turning to the results of the theory of integral equations the user can easily identify circumstances which guarantee the existence of the required waves and can decide if the wave has a sharp front or not. Models with the same characteristics arise in several scientific fields, for example heat transfer, combustion, reaction chemistry, plasma physics, etc.
Please contact:
Róbert Kersner - SZTAKI
Tel: +36 1 4665 783
E-mail: kersner@sztaki.hu
