ERCIM News No.25 - April 1996 - CNR

TAn ­p; A New Multiresolution Volume Visualization System


by Claudio Montani, Enrico Puppo and Roberto Scopigno

The main problems in volume dataset visualization are the excessive data complexity, which limits interactivity, and the lack of generality and integration of the rendering solutions. Moreover, Volume Visualization systems often manage only a single class of data (e.g. regular or curvilinear). TAn (Tetrahedra Analyzer) is a new prototypal system for Volume Visualization, designed to cope with data complexity. TAn supports multiresolution modelling and visualization of volume datasets by adopting an innovative representation based on tetrahedral decomposition. No limitations are imposed on the classes of data that can be managed: TAn processes regular, curvilinear and scattered data. The tetrahedral decomposition adopted is also an effective choice for the design of integrated visualization methods.

Volume Visualization is now recognized as a major subfield of Scientific Visualization. This discipline entails the management of datasets generically defined as the result of a measure over a discrete set of sites in the 3D space. Volume datasets are usually classified according to the distribution of the sampling sites in the 3D space. A number of techniques have been proposed to visualize such data efficiently.

A problem common to all classes of datasets is the huge amount of data involved; this affects both storage requirements and visualization times. Dataset complexity has been taken into account in a number of recent proposals to reduce visualization times, but the techniques developed are designed mainly for regular volume datasets.

A more general approach consists in using approximated representations of the dataset, defined on meshes at reduced resolutions, in order to allow fast visualization when high accuracy is not needed. The idea is to work on data simplification rather than on graphics output simplification. Given a rule for simplifying the dataset, a multiresolution representation can be simply achieved by applying this rule with different approximation parameters; this can effectively improve the efficiency of data rendering.

Naive ways to achieve multiresolution, like subsampling or averaging have several limitations: they only control the size of the reduced dataset but not its accuracy with respect to the original dataset; they are not adaptive, i.e., they do not permit a variable data density to be maintained over different regions of the domain, according to the variations of the scalar field represented; they are only suitable for regularly gridded data.

In a recent paper, we proposed a methodology for building and manipulating volume representations at multiple resolution. Our multiresolutions model is based on tetrahedral decompositions with scattered vertices, which can be obtained from any initial dataset. Tetrahedral meshes have been widely used to represent irregular volume data. In the context of volume visualization, a number of rendering techniques have been proposed which are well-suited for tetrahedralized datasets.

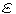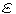Multiresolution is achieved through a compact model that incorporates a whole sequence of tetrahedral decompositions, corresponding to increasingly accurate approximations of the original dataset. Given a threshold for the approximation error, the model is able to provide a tetrahedralization based on a minimally sufficient subset of the sites that achieves an accuracy of in approximating the original dataset. The model is built through an adaptive incremental approach driven by local coherence. The key idea behind our model is that a high number of different decompositions at increasing accuracy can be obtained on the basis of a moderate number of tetrahedral cells. Different tetra-hedralizations are not stored independently: a unique data structure embeds them all, and a simple but efficient algorithm extracts each single model on-line at any arbitrary tolerance .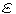

A prototypal volume visualization system, TAn (Tetrahedra Analyzer), was designed which adopts the proposed multiresolution tetrahedral representation: a compact representation scheme which stores all the intermediate steps of a progressively refining 3D triangulation process. Dataset triangulation is performed only once, as a preprocessing phase. The results of this incremental refinement process are saved on a file (known as the history file). At run time, TAn allows the user to choose the tolerance; a tessellated representation of the dataset which satisfies the specified tolerance is then extracted from the history data.

Projective rendering approaches have been adopted.

The main features of TAn are:
The TAn system works on SGI workstations and adopts OpenGL and the XForms user interface toolkit for graphics output and GUI design.

Availability

TAn is the result of a scientific cooperation between three CNR Institutes: CNUCE and IEI, Pisa, and IMA, Genoa.

The TAn system has been released in the public domain. The software, compiled for SGI workstations, and a downloadable preprint of the paper that describes the data representation scheme adopted are available on our World Wide Web site at URL:
http://miles.cnuce.cnr.it/cg/homepage.html

Future Plans

Our research on volume data management and rendering will continue. We are working on the extension of some of the techniques provided in the current TAn release:
Please contact:
Roberto Scopigno ­p; CNUCE-CNR
Tel: +39 50 593304
Email: scopigno@cnuce.cnr.it
return to the contents page