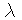During the software development process, specification, design and proof search methodologies are essential and have an impact on the activities of verification and validation and then on the quality of the obtained software. Our approach to this problem consists in representing concepts and development steps with appropriate logics and formal methods. For an effective use of formal techniques based on logics, works on formal specification, automated deduction and computer-aided proof development, proof analysis and proof search algorithms are necessary.
Logics are involved in software design and computer science in general to give proof-theoretical foundations, methods to represent and to solve some classes of problems. The mechanization of deductive systems that allow to establish the syntactic, semantic and algorithmic properties and to characterize the classes of problems is important. Such systems also allow to represent some complex reasoning, for instance with modalities or resources managements. Linear logic is a good example of the interaction between proof theory and computer science in the context of bounded resources management. It allows to integrate a dynamic into proof systems and has an impact on new proposals of proof theory dedicated to programming methods. Computing the type of a program is a proof of partial correctness and a type can be considered as a specification. The type theory, with the Curry-Howard isomorphism between lambda-terms and intuitonistic proofs is an important conceptual tool for programming (language definition, validity properties, program synthesis).
In our project, we want to consider the design and the analysis of systems through proof theory and its relationship with computing through the two important paradigms proofs-as-programs and proof-search as computation. Thus, some important and complementary points are considered : determinating logical fragments to modelize programming concepts, analyzing the structure of the proofs in such fragments and proposing methods and tools for proof management. It constitutes a particular methodology around the {\em proof} object that could be specialized and adapted for given application domains leading to extensions or refinements and new theoretical and implementation problems. A consequence of this approach is that we consider different formal systems from type theory and intuitionistic, classical or linear logics, that allow to represent and to analyze concepts, at a logical level, such as communication, concurrency, sequentiality, control or verification of systems properties. They have in common to be constructive, to express actions through the notion of proof and to induce also a relationship between proofs and programs. In this context, linear logic has a particular status. In fact, this constructive and symmetrical logic can represent in a finer way various programming concepts, by considering proofs as actions. For example, the notion of proof-net leads to a better structural analysis of proofs. A main point, that is the interest and the difficulty of the approach, is the strong interaction between the works on the semantics and structure of proofs, on the algorithmic content of proofs and on the algorithms for efficiency proof search. The implementation of these results is an effective part of our work and leads to proposals of specific tools or methods (strategies, proof plans) to obtain efficient systems for proof development.
In this context, the different objectives of the TYPES project can be summarized by the following topics :
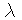-calculi). An important point is to master the automation and the complexity of the proposed technics.
The results will be applied and specialized in domains as the design of process calculi based on proof theory of linear logic, the automated analysis of sentences in natural language, the diagnosis of actions and the synchronization of activities in a network.
loria.fr