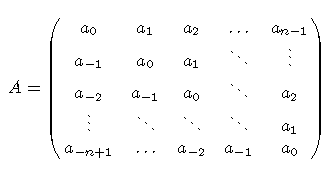
An example of an n x n Toeplitz matrix

by Dario Bini
Toeplitz matrices are matrices having constant entries along their diagonals. This structure is very interesting in itself for all the rich theoretical properties which it involves, but at the same time it is important for the dramatic impact that it has in applications.
Toeplitz matrices arise in many different theoretical and applicative fields, in the mathematical modelling of all the problems where some sort of shift invariance occurs in terms of space or of time. This shift invariance is reflected in the structure of the matrix itself where a south-eastern shift of the entries leaves the matrix unchanged. The Toeplitz structure may occurr entry-wise, for one-dimensional problems, or block-wise, for two-dimensional problems, or even at several nested levels in multidimensional problems. Toeplitz matrices may be finite or even infinite according to the features of the problem that is modelled.
Problems Modelled by Toeplitz Matrices
Typical problems modelled by Toeplitz matrices are: the numerical solution of certain differential equations, and certain integral equations (regularization of inverse problems); the computation of spline functions; time series analysis; signal and image processing; Markov chains and queueing theory; polynomial and power series computations. Other problems involve Toeplitz-like matrices, or matrices having a displacement structure (Hankel, Bezout, Cauchy, Hilbert, Loewner and Frobenius matrices).
There is a natural one-to-one correspondence between problems involving Toeplitz-like structures and polynomials (power series) which allows shifting from algorithms for Toeplitz-like computations to algorithms for polynomial (power series) computations and viceversa. In this way Fast Fourier Transform (FFT) becomes a fundamental tool for all the computations involving Toeplitz-like matrices.
Current Research
Research in the field of the analysis of algorithms for Toeplitz (-like) matrices is very active and has shown interesting advances over the last years. In particular, these have regarded two specific problems:
Considerable progress has been achieved in the last decade with the introduction of algorithms based on the "preconditioned conjugate gradient method" (PCG). Such algorithms have reached a high degree of efficiency and reliability, due to the accurate choice of the preconditioner. They are thus far more suitable for matrices generated by real functions than the so-called superfast direct algorithms. Also, unlike the latter, they can be efficiently implemented on parallel architectures, since the whole computation is simply reduced to a few FFT's.
The key point of PCG algorithms is to devise a good preconditioner in such a way that the preconditioned matrix has almost all the eigenvalues clustered around 1. In this case the conjugate gradient algorithm applied to the preconditioned matrix converges in a few steps. For Toeplitz matrices an efficient choice of the preconditioner can be performed within suitable algebras of matrices like circulant matrices, the Hartley algebra and the class 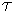 , which are naturally associated with Fourier, Hartley and Sine discrete transforms, respectively. This can be obtained by means of a suitable functional approximation of the function f(z) associated with the original matrix.
, which are naturally associated with Fourier, Hartley and Sine discrete transforms, respectively. This can be obtained by means of a suitable functional approximation of the function f(z) associated with the original matrix.
Research performed in this field has led to solving not only the (easy) problem where the function f(z) is positive, but also the asymptotically ill conditioned case where f(z) is non-negative and there exists z0 such that f(z0)=0, and more generally, the case where f(z) has non-definite sign and thus the associated matrix is not positive definite.
Solving a Problem in Queueing Theory
The computation of the invariant vector of a stochastic matrix of the M/G/1 type, i.e., a block Toeplitz-like infinite matrix in Hessenberg form, involves more delicate problems. This is mainly due to the infinite features of the problem. No direct methods are available in this case, and the most used solution techniques are based on matrix functional iterations (fixed-point). Such methods implicitly (but not fully) use the Toeplitz structure without exploiting the acceleration allowed by the FFT. Moreover they have a linear convergence.
Recently a powerful and efficient technique, which fully exploits the Toeplitz structure, has been introduced and has lead to an algorithm of low complexity which converges quadratically to the solution. This technique is based on rephrasing the problem in terms of matrix power series and on applying a divide-and-conquer strategy together with FFT. The resulting algorithm has resulted in a dramatic reduction in the time needed for the solution of concrete network problems.