Diederik Johannes Korteweg at the age of 80 in 1928

by Henk Nieland
Hundred years ago an article appeared in the well-known British journal Philosophical Magazine, written by the Dutch mathematicians Korteweg and De Vries. It described the behaviour of certain types of waves occurring in a shallow canal in terms of a non-linear differential equation. This equation, now known as the Korteweg - De Vries equation (KdV), has played a central role in the study of non-linear phenomena, which has flourished so much since the 1970s. The world's leading experts in the field gathered 24-26 April 1995 at CWI to celebrate this centennial.
Diederik Johannes Korteweg
at the age of 80 in 1928
The article was based on De Vries' Ph.D. thesis, in which he proved that the 'solitary wave', discovered and described by the Scottish engineer John Scott Russell about half a century earlier, really could keep its form. Many scientists, including Lord Rayleigh, had believed that this wave too would smooth out in the long run, as it should according to `linear science', such as the waves caused by a stone thrown in a pond. However, the KdV-equation contains a non-linear part which compensates this dispersive effect.
The KdV-equation remained in obscurity until 1965, when Zabusky and Kruskal (both speakers at the centennial symposium) discovered that two such solitary waves, or `solitons', emerge unchanged from a collision. The discovery of this remarkable stability property caused a - still ongoing - tide of research (sometimes called the `soliton revolution'). Two years later, Gardner, Greene, Kruskal and Miura invented the Inverse Spectral Transform to solve the Cauchy problem for KdV, and with this method Zakharov and Faddeev (both speakers in Amsterdam) proved in 1971 the complete integrability of KdV.
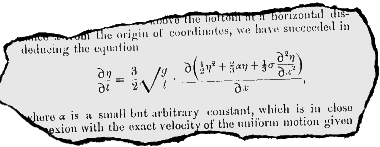
The Korteweg - De Vries equation, as published in the Philosophical Magazine, 1895, fifth series, Volume XXXIX, p. 422-433
These far-reaching breakthroughs had an enormous impact on the development of modern non-linear mathematical science. Whereas many applications of KdV theory are in fluid mechanics - not surprising because in this discipline several key non-linear structures, such as shocks, bifurcations, solitons, deterministic chaos, and hypercomplex systems were first discovered - , also vast areas of mathematics (ordinary differential equations, algebraic geometry, Lie group theory, differential geometry, asymptotics) and theoretical physics (quantum field theory, string and conformal field theory, quantum gravity, classical general relativity) opened up as a consequence of the basic research into the KdV-equation.
With KdV as a prototype, research into other famous integrable systems such as the Non-linear Schrödinger equation and the Sine-Gordon equation, has led to applications ranging from condensed matter and semi-conductor physics through non-linear optics and laser physics, hydrodynamics, meteorology and plasma physics to protein systems and neurophysiology. Examples highlighted at the symposium included internal solitons in the ocean, the transport of magma from the Earth's interior to the surface, non-linear acoustics of bubbly liquids, the Great Red Spot and other features in the Jovian atmosphere, and ion-acoustic plasma waves.
The most spectacular application so far was highlighted at the symposium by Hasegawa (Osaka): the use of optical solitons in fibres as an efficient (reliable and fast) means of long-distance communication. Proposed already more than twenty years ago by Tappert and Hasegawa (then at Bell Labs), these solitons are the best long-distance information carriers discovered so far. Recently 20 Gigabit/s soliton signals were transmitted error-free over a distance of 14.000 kilometers in a loop experiment. In a concrete project, 60 billion dollar is being invested in transatlantic optical fibre communication.
In the extensive obituary of Korteweg in the 1945/1946 Annals of the Royal Dutch Academy of Arts and Science, the KdV-equation is not even mentioned. Apparently at that time nobody could foresee that fifty years later articles with the acronym KdV would be counted by thousands.